Tractrix

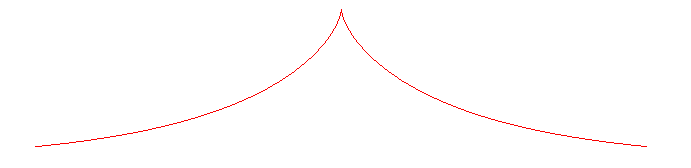
TRACTRIX

Curve considered by Claude Perrault in 1670, then studied by Newton in 1676, Huygens in 1692 and Leibniz in 1693.
Other name: equitangential curve (because the tangent:T is constant along this curve)

Differential equation:

, i.e.

.
Cartesian parametrization:

where

(gd is the Gudermannian function).
Or also

.
Cartesian equation:

.
Transcendental curve.
Curvilinear abscissa:

. Cartesian tangential angle:

.
Radius of curvature:

.
Intrinsic equation 1:

. Intrinsic equation 2:

.
Area between the curve and the asymptote:

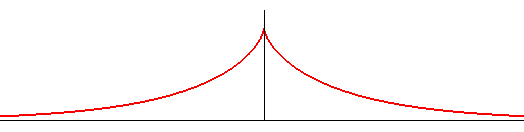(area of the semicircle with centre O passing by the cuspidal point; see here a nice animation of this fact).

The tractrix can be defined as a tractory of the line, or, which amounts to the same thing, as a curve with constant tangent.

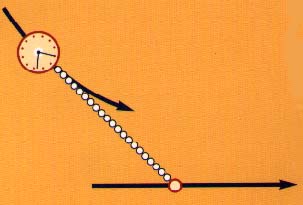
The initial problem posed by Claude Perrault was to find the trajectory of a clock attached to a catenary the end of which describes the edge of a table. Nowadays, the image would rather be that of the trajectory of the back wheels of a vehicle the front wheels of which describe a line.

The tractrix is also:

- the principal involute of the catenary (i.e. involute the cuspidal point of which is at the summit of the catenary); here, the equation of the catenary is .

- the locus of the points by which pass a tangent to the logarithmic curve: as well as a tangent to the symmetric logarithmic curve: that are perpendicular. In other words, the tractrix is the orthoptic of the reunion of these two logarithmic curves.
Opposite, in blue and yellow, the two logarithmic curves, in red the corresponding tractrix, and in green the catenary, median of the two logarithmic curves.

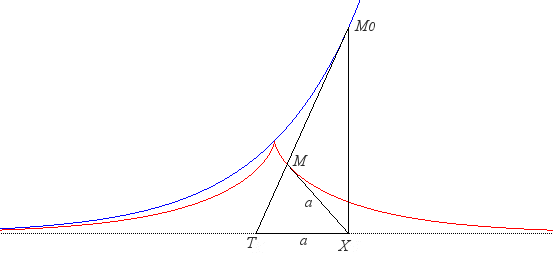
- the locus of a point M constructed as follows: point M₀ describing the logarithmic curve , let X be the projection on
Ox and T the intersection of the tangent with Ox. We know that the "subtangent" TX is constant equal to a. The
point M is the point of [M₀T] such that MX = a; the line (MX) then wraps the tractrix.
(Construction due to Pietro Milici, linked to the previous one).

- The locus of the centre of a hyperbolic spiral rolling without slipping on a line (it is therefore a roulette).

Furthermore, the orthogonal trajectories of the family of circles centred on Ox with radius a are translated tractrices.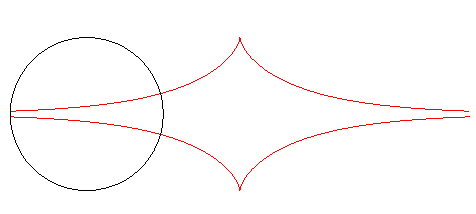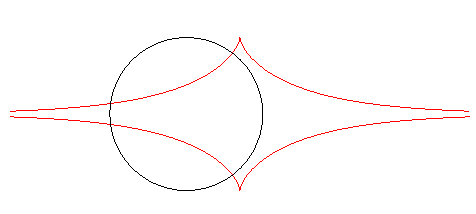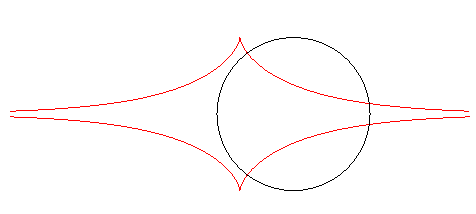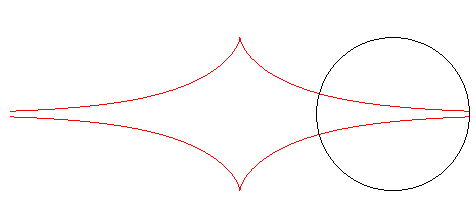

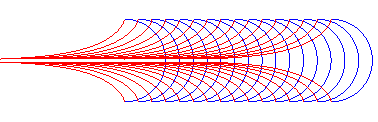The pedal of the tractrix with respect to O is the elegant curve parametrized by
looking like the regular bifolium.

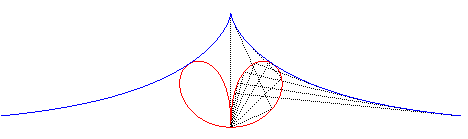The radial curve of the tractrix is the kappa.
Its rotation around the base generates the pseudo-sphere.
See also the syntractrices.
Remark: the curves with constant normal are none other than the circles.

Instrument due to Perks to draw the tractrix.

next curve previous curve 2D curves 3D curves surfaces fractals polyhedra

- the principal involute of the catenary (i.e. involute the cuspidal point of which is at the summit of the catenary); here, the equation of the catenary is .
- the locus of the points by which pass a tangent to the logarithmic curve: as well as a tangent to the symmetric logarithmic curve: that are perpendicular. In other words, the tractrix is the orthoptic of the reunion of these two logarithmic curves. Opposite, in blue and yellow, the two logarithmic curves, in red the corresponding tractrix, and in green the catenary, median of the two logarithmic curves.
- the locus of a point M constructed as follows: point M₀ describing the logarithmic curve , let X be the projection on Ox and T the intersection of the tangent with Ox. We know that the "subtangent" TX is constant equal to a. The point M is the point of [M₀T] such that MX = a; the line (MX) then wraps the tractrix. (Construction due to Pietro Milici, linked to the previous one).
- The locus of the centre of a hyperbolic spiral rolling without slipping on a line (it is therefore a roulette).