BOUTEILLE DE KLEIN
Klein bottle,
Kleinsche Flasche
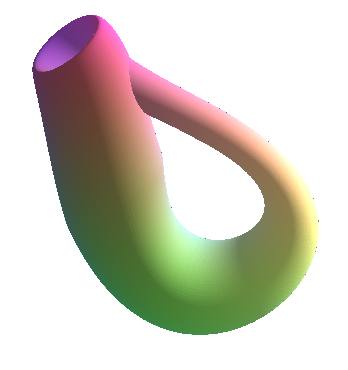
lien vers une figure
manipulable à la souris
| surface suivante | surface précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
BOUTEILLE DE KLEIN
Klein bottle,
Kleinsche Flasche
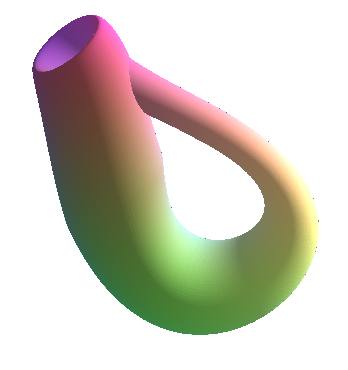
lien vers une figure
manipulable à la souris
| Paramétrisation sans point singulier dans Paramétrisation donnant la forme classique dans Première partie : Deuxième partie : Paramétrisation en tore sinusoïdal (projection 3D de la surface 4D ci-dessus) : Rotation d'un huit avec retournement : Équation cartésienne polynomiale de Ian Stewart : Voir ici une méthode générale de création de bouteille de Klein. |
| On désigne par bouteille de Klein, notée |
 |
|
| Si l'on identifie d'abord les deux côtés de même sens (concrètement, si on les coud bord à bord), on obtient un tronc de cylindre ; la bouteille de Klein est donc un tronc de cylindre dont les deux bords sont identifiés avec inversion du sens. |
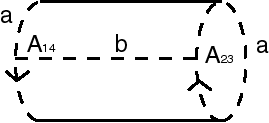 |
|
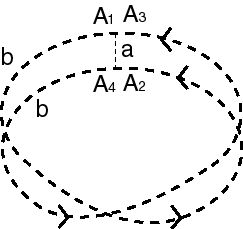
| Si l'on identifie d'abord les deux côtés de sens contraire, on obtient un ruban de Möbius. La bouteille de Klein est donc un ruban de Möbius dont les deux demi-bords sont identifiés dans le même sens. (Si on les identifie en sens contraire, on obtient un plan projectif). |
 |
|
| En utilisant la représentation triangulaire du ruban de Möbius, et en identifiant 2 demi-bases inféreures du triangle dans le même sens, on obtient alors la représentation ci-contre de la bouteille de Klein... | 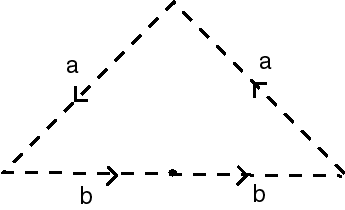 |
|
| ...représentation montrant que la bouteille de Klein est aussi la surface obtenue en cousant deux rubans de Möbius bord à bord. |  |
|
| Vue montrant qu'une demi-bouteille de Klein est bien
un ruban de Möbius.
|
 |
|
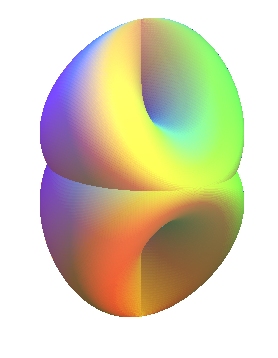
| De plus, le ruban de Möbius étant un plan
projectif troué, la bouteille de Klein est donc aussi la somme
connexe de deux plans
projectifs réels.
On en obtient donc une autre représentation en accolant deux bonnets croisés ouverts (au centre). A droite, quartique d'équation
|
 |
 |
Le ruban de Möbius est une surface unilatère
(à une seule face), donc non orientable, de genre
2, de caractéristique
d'Euler-Poincaré :
nulle, et de nombre chromatique
6 comme le tore:(et
non 7 comme le voudrait la formule de Heawood
)
:
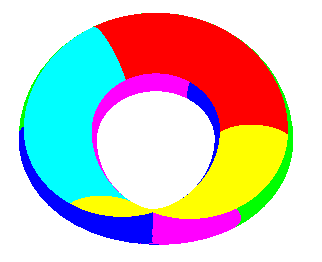
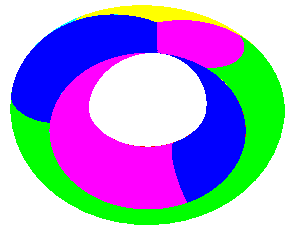
Elle ne peut pas être plongée dans R3, mais seulement immergée avec auto-intersection.
Si la représentation classique ressemble bien à une bouteille (dans laquelle on évitera de mettre du liquide !),
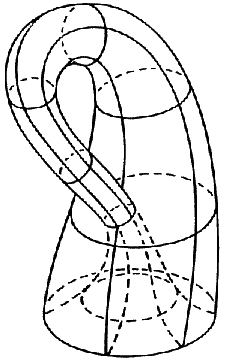
Les 3 représentations suivantes de la bouteille
de Klein utilisant ce procédé sont plus symétriques
que la représentation classique, mais présentent le défaut
de ne pas avoir de plan tangent bien défini en certains points :
 |
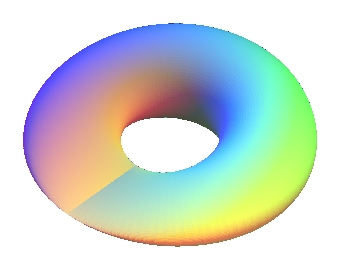 |
 |
| Collage d'un demi tore avec un demi
dôme de Bohème.
Il y a deux points cuspidaux. |
Tore sinusoïdal.
Deux points cuspidaux également. |
Tube d'âme une quartique
piriforme.
Il y a une ligne cuspidale. |
| Rotation d'un huit avec un demi-tour ; on obtient cette fois une vraie immersion de la bouteille de Klein, plus du tout en forme de bouteille ! |
 |
 |
| La première représentation permet de bien voir comment la bouteille de Klein est obtenue en identifiant deux demi-bords d'un ruban de Möbius : |  |
La deuxième représentation permet, elle, de bien voir comment la bouteille de Klein est obtenue en cousant bord à bord deux rubans de Möbius.
 +
+ |
 =
= |
 |
Dans ,
on peut par contre effectuer le mouvement d'un cercle avec retournement
sans que la surface obtenue ne présente d'auto-intersection (voir
la paramétrisation dans l'encadré ci-dessus).
Voici enfin un modèle polyédrique de la bouteille de Klein :
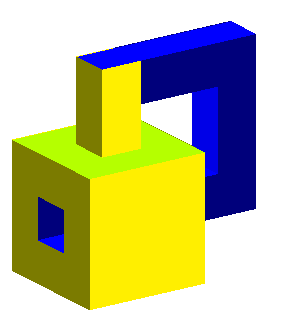
Si l'on peint la bouteille de Klein, la pellicule de peinture
(qui est d'un seul tenant puisque cette surface est unilatère) obtenue
est une immersion du tore (autrement dit, le revêtement
à deux feuillets est le tore); c'est la raison pour laquelle
la bouteille de Klein a été utilisée comme étape
centrale du retournement du tore : voir par exemple, ce
texte de Pour la Science.
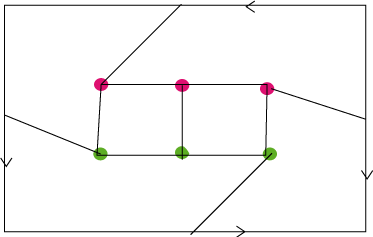
| Le problème
des trois maisons et des trois usines est soluble sur la bouteille
de Klein, contrairement au plan. En d'autre termes, on peut tracer sans
croisement d'arêtes le graphe biparti Idem pour le graphe complet à 5 sommets |
 |
La bouteille de Klein percée (caractérisée
par le fait d'être une surface unilatère à un bord
de genre 2) peut être représentée
par le slip de Möbius (Möbius shorts en anglais)
: on l'obtient en reliant un ruban fermé non torsadé par
une bande comme ci-dessous :
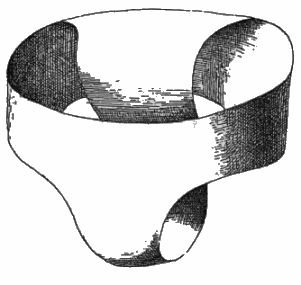
Ce slip impossible à enfiler est une bouteille de Klein percée ! |
 |
| De même que le ruban de Möbius peut être
généralisé en un ruban à n demi-tours
(et l'on obtient topologiquement un ruban de Möbius seulement quand
n
est
impair), la bouteille de Klein peut être généralisée
en une bouteille à n retournements, qui n'est topologiquement
une bouteille de Klein que lorsque n est impair.
Ci-contre, les bouteilles multiples ont été crées à partir d'un tube de section variable d'âme une épicycloïde. |
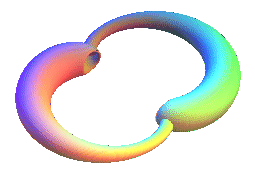
 |
La bouteille de Klein permet aux infographistes de montrer leur talent :
LIENS :
www.geom.uiuc.edu/~banchoff/Klein4D/Klein4D.html
Jeux sur une bouteille de Klein : geometrygames.org/TorusGames/index.html
Pour acheter des bouteilles de Klein en verre et même un bonnet
de Klein ! : www.kleinbottle.com
| surface suivante | surface précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2013