CARACTÉRISTIQUE D'EULER-POINCARÉ D'UNE VARIÉTÉ
Euler
characteristic of a surface, eulersche Charakteristik einer Varietät
NOMBRE CHROMATIQUE D'UNE SURFACE
Chromatic
number of a surface, kromatische Zahl einer Fläche
| surface suivante | surface précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
CARACTÉRISTIQUE D'EULER-POINCARÉ D'UNE VARIÉTÉ
Euler
characteristic of a surface, eulersche Charakteristik einer Varietät
NOMBRE CHROMATIQUE D'UNE SURFACE
Chromatic
number of a surface, kromatische Zahl einer Fläche
et qui est réunion finie de parties homéomorphes à
de telles boules) est une partition finie de cette surface en sous-ensembles
homéomorphes à 
pour p 
n.
le nombre des sous-ensembles homéomorphes à ,
on démontre que le nombre : 
est indépendant de la décomposition cellulaire ; il est appelé
caractéristique
d'Euler-Poincaré de la variété. C'est un invariant
topologique.
La caractéristique d'Euler-Poincaré est "réunion-additive", à savoir que la caractéristique d'une variété qui est réunion disjointe de deux variétés est la somme des caractéristiques de ces deux variétés.
Exemples :
La caractéristique de 
et de toutes ses boules ouvertes est 
(1 pour le point, –1 pour la droite ou un intervalle ouvert, 1 pour le
plan ou un disque ouvert , –1 pour 
et ses boules ouvertes).
La caractéristique de 
(sphère de 
)
, réunion d'une copie de
et d'un point, est (–1)n
+ 1 (0 pour le cercle ou toute courbe de Jordan, 2 pour la sphère 
et toutes les surfaces qui lui sont homéomorphes).
La caractéristique d'une boule fermée non
réduite à un point de
(réunion d'une boule ouverte et d'une copie de 
)
est 1 ; ceci vaut donc pour un segment ou un disque fermé).
La caractéristique du cylindre (plan + droite) est nulle, donc aussi celle du cylindre à un ou deux bords, du ruban de Möbius (qu'il soit fermé ou ouvert), du tore et de la bouteille de Klein.
La caractéristique du plan projectif est 1 (ruban de Möbius ouvert plus un point).
La caractéristique d'Euler-Poincaré d'une
somme connexe de deux surfaces est
donnée par la relation 
(perte de deux disques ouverts) ; on obtient ainsi la caractéristique
d'Euler-Poincaré de toute surface close.
Elle vaut 2 – 2n pour le tore
à n anses :
et 2 – n pour la sphère munie de n bonnets
croisés : 
.
Plus généralement, la caractéristique
de la sphère munie de p anses, de q bonnets croisés
et percée r fois (d'un disque ouvert, ou fermé) vaut 
;
ceci donne donc la caractéristique de toute surface connexe de type
fini.
Deux surfaces connexes orientables (resp. non orientables) ayant le même nombre de bords sont homéomorphes si et seulement si elles ont même caractéristique.
La caractéristique d'Euler-Poincaré d'une surface de type fini peut se calculer par divers moyens.
Une décomposition cellulaire de la surface est
ici une partition finie de cette surface en sous-ensembles homéomorphes
au plan (les faces, en nombre F), à la droite (les
arêtes,
en nombre A), ou au point (les sommets, en nombre S) et la
caractéristique d'Euler-Poincaré se calcule par la relation 
.
  =
2
- 4 + 4 = 2. |
 = 4
-
8 + 4 = 0. |
 = 3-
6 + 4 = 1.
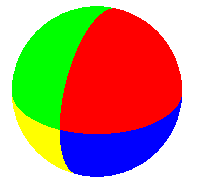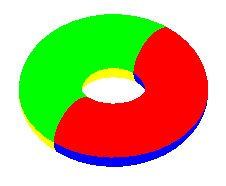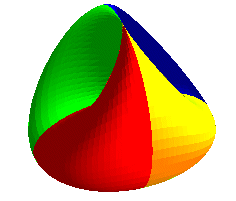(Il faut compter deux fois l'arête double) |
Mais la caractéristique d'Euler-Poincaré
peut aussi se calculer par la relation du montagnard : si la surface
est immergée dans R3
et
que la fonction altitude possède un nombre fini de singularités
qui sont des fonds (en nombre f), des sommets (en nombre s)
ou des cols (en nombre c), la caractéristique d'Euler Poincaré
est 
.
Pour la sphère,
 = 1
- 0 + 1 = 2. |
Pour le tore,
= 1-
2 + 1 = 0. |
Pour le plan projectif,
= 1-
0 + 0 = 1. |
Pour la bouteille de Klein,
= 1
- 1 + 0 = 0. |
Elle est aussi égale à la somme des indices
des singularités d'un champ de vecteurs à nombre fini de
singularités tracé sur la surface (théorème
de Hopf).
  |
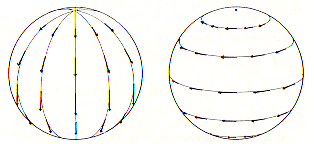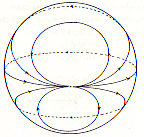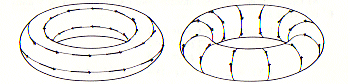
Pour le tore, pas de singularité :
|
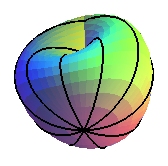
Pour le plan projectif, une singularité d'indice 1 c = 1. |
Pour la bouteille de Klein, pas de singularité : c = 0. |
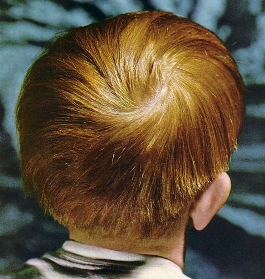
Un champ de vecteurs sur une surface de caractéristique non nulle possède donc au moins une singularité ; par exemple, on ne peut pas coiffer une sphère chevelue sans singularité.
La caractéristique d'Euler-Poincaré peut enfin se calculer à partir de la courbure par la formule de Gauss-Bonnet.
Une carte tracée sur la surface est une
décomposition cellulaire telle qu'à chaque sommet aboutisse
au moins trois arêtes ; le nombre chromatique C d'une
surface de type fini est le nombre minimal de couleurs nécessaires
pour colorier les faces d'une carte de sorte que deux faces ayant au moins
une arête commune soient de couleur distinctes ; ce nombre est supérieur
ou égal au nombre K, nombre maximal de faces d'une carte
dont les faces ont toutes 2 à 2 au moins une arête commune.
En écrivant que pour une carte,
,
on obtient à l'aide de la relation d'Euler-Poincaré l'inégalité 
,
qui pour une carte à K faces 2 à 2 contigües,
ayant donc A = K (K – 1)/2 arêtes et vérfiant
S
= F = K, donne l'inégalité 
,
soit 
(nombre de Heawood).
Il a été démontré, que, bizarrement
à l'exception de la bouteille de
Klein, ces trois nombres C,
K et 
, vérifiant à priori 
sont égaux :
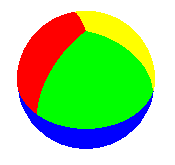
Carte à K = 4 pays deux à deux contigus sur la sphère |
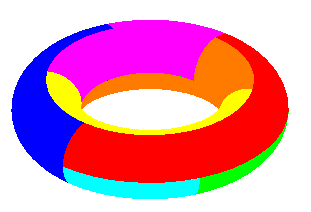
Carte à K = 7 pays deux à deux contigus sur le tore |
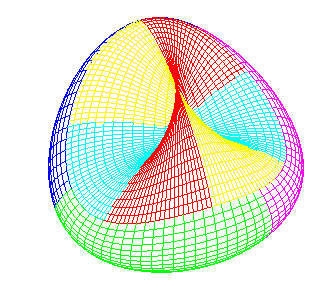
Carte à K = 6 pays deux à deux contigus sur le plan projectif |
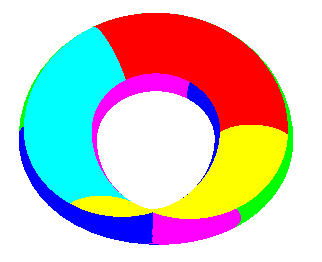
Carte à K = 6 pays deux à deux contigus sur la bouteille de Klein |
| Surface | genre g | car. d'E.-P.  |
nombre de Heawood H( ) |
nombre chromatique C | K |
| sphère | 0 | 2 | 4 | 4 | 4 |
| plan projectif | 1 | 1 | 6 | 6 | 6 |
| bouteille de Klein | 2 | 0 | 7 | 6 | 6 |
| tore | 1 | 0 | 7 | 7 | 7 |
| surface de Dyck | 3 | –1 | 7 | 7 | 7 |
| bouteille de Klein munie d'une anse, sphère munie de 4 bonnets croisés | 4 | –2 | 8 | 8 | 8 |
| tore à deux trous | 2 | –2 | 8 | 8 | 8 |
tore à n trous,  |
n | 2 – 2n |  |
|
|
| plan projectif muni de n anses, sphère munie de 2n + 1 bonnets croisés | 2n + 1 | 1 – 2n |  |
|
|
| bouteille de Klein munie de n anses, sphère munie de 2n + 2 bonnets croisés | 2n + 2 | –2n |  |
|
|
| surface suivante | surface précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2023