For example, the "normal" strip opposite is orientable, whereas the Möbius strip is not.
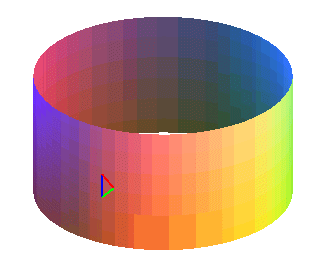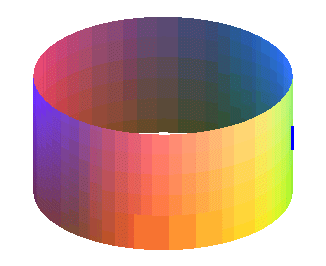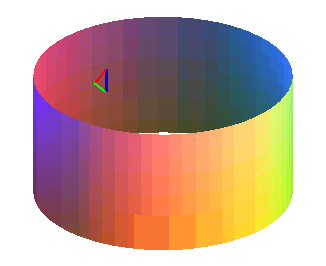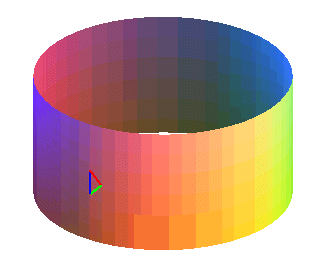
The triangle keeps its orientation.
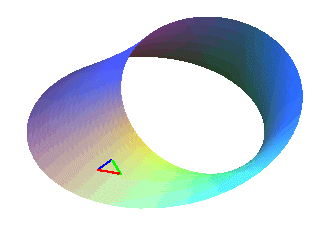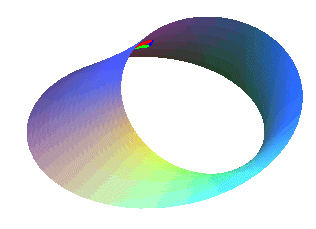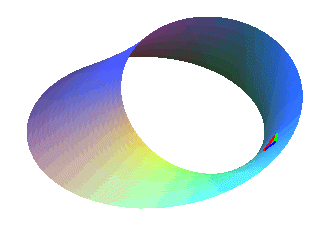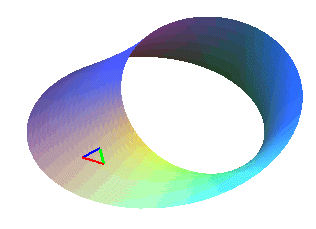
With each turn, the triangle changes orientation ("red green blue" becomes "red blue green" and vice-versa).

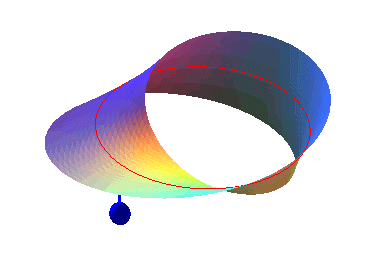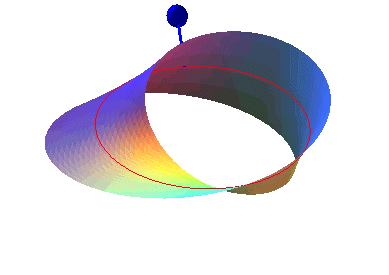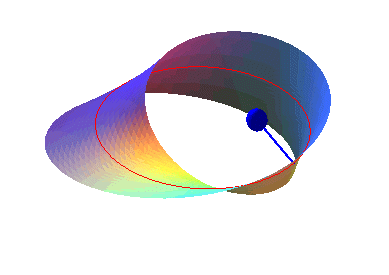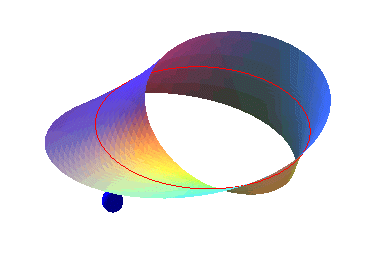
He can.
| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
ORIENTABLE, ONE-SIDED SURFACE
| Wikipedia article. |
| A connected surface is said to be orientable if the oriented triangle (ABC) included in this surface cannot be continuously transformed into coinciding with the triangle oriented in the opposite way (ACB); then, there are two types of orientations of triangles.
In the non-orientable case, all the oriented triangles can be superimposed.
For example, the "normal" strip opposite is orientable, whereas the Möbius strip is not. |
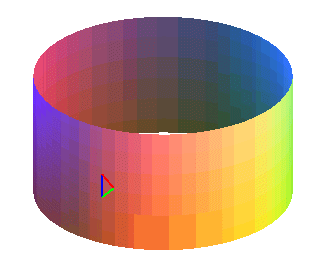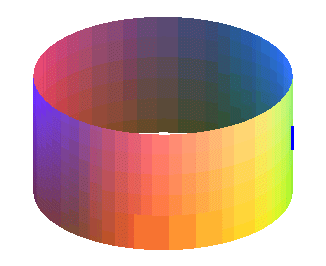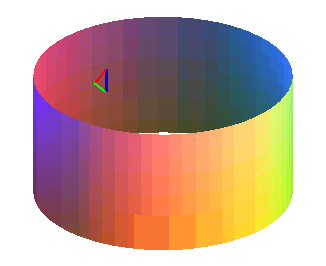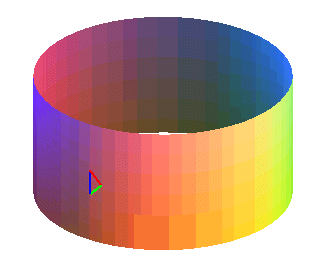
The triangle keeps its orientation. |
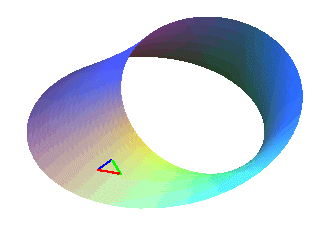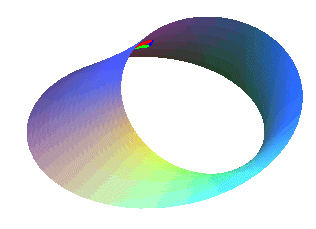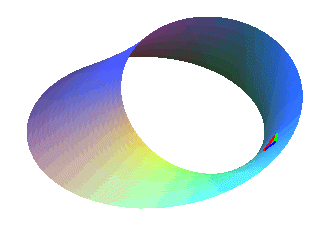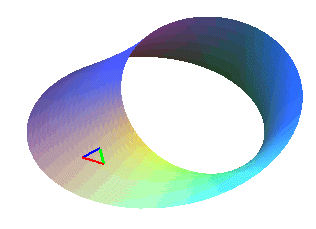
With each turn, the triangle changes orientation ("red green blue" becomes "red blue green" and vice-versa). |
| Embedded in the Euclidian space |

|
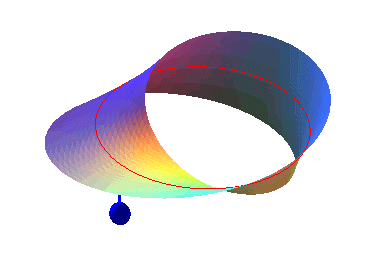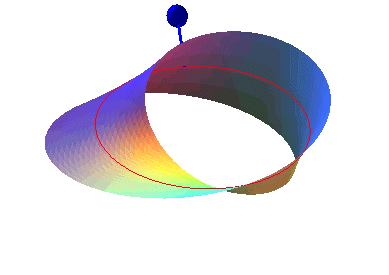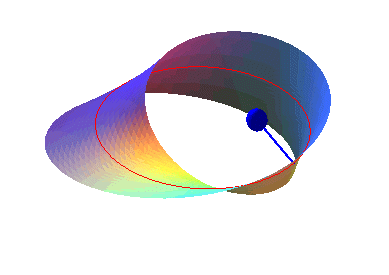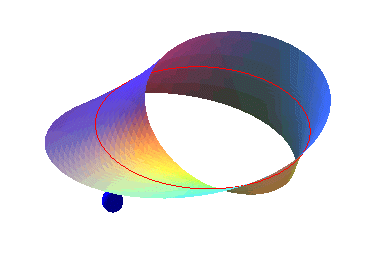
He can. |
See also the Euler characteristic.
| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017