POLYÈDRE DE CSASZAR
Csaszar's polyhedron, Csaszarsches Polyeder
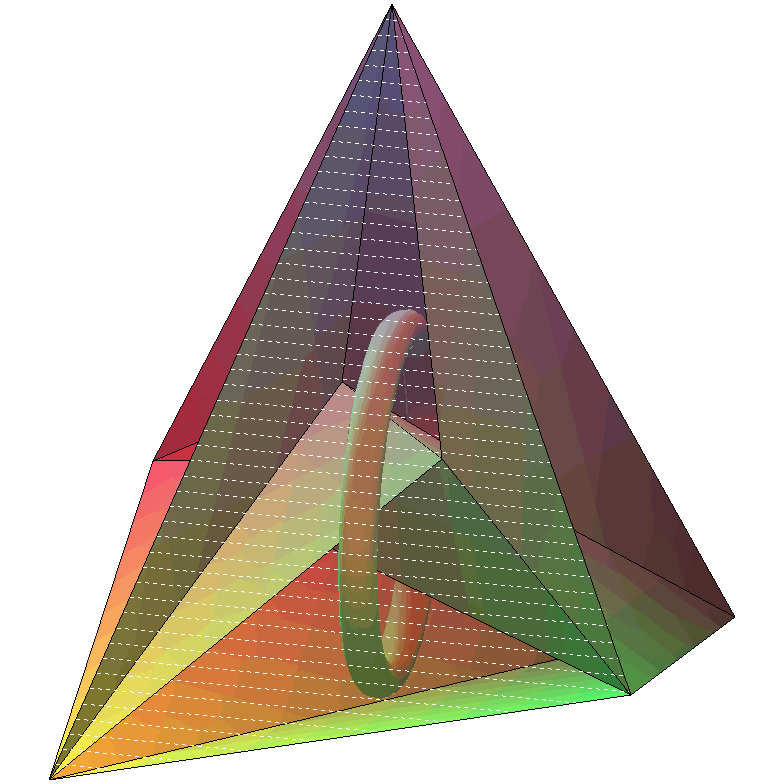
| polyèdre suivant | polyèdre précédent | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
POLYÈDRE DE CSASZAR
Csaszar's polyhedron, Csaszarsches Polyeder
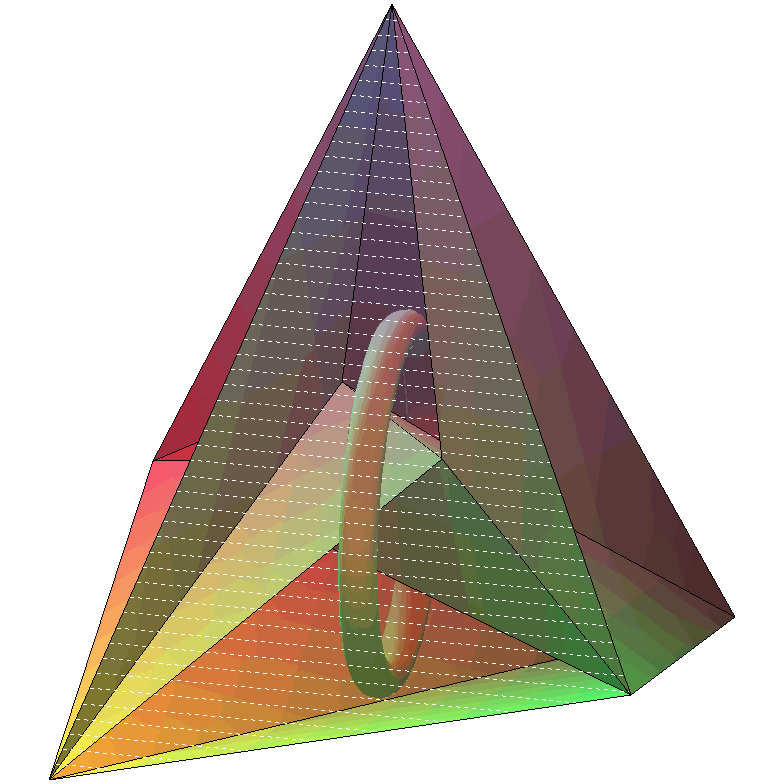

| Akos
Csaszar (1924-2017) : Mathématicien hongrois.
Polyèdre découvert en 1949. Lien vers un patron réalisé par Jean-Jacques Dupas. Figure ci-dessus avec une face transparente réalisée par Alain Esculier. |
Le polyèdre de Csaszar est un polyèdre
à 7 sommets, 14 faces triangulaires et 21 arêtes, de genre
1 (ou torique, i.e. dont la surface est homéomorphe au
tore)
tel que chaque sommet est relié par une arête aux 6 autres
(autrement dit le graphe associé
est complet).
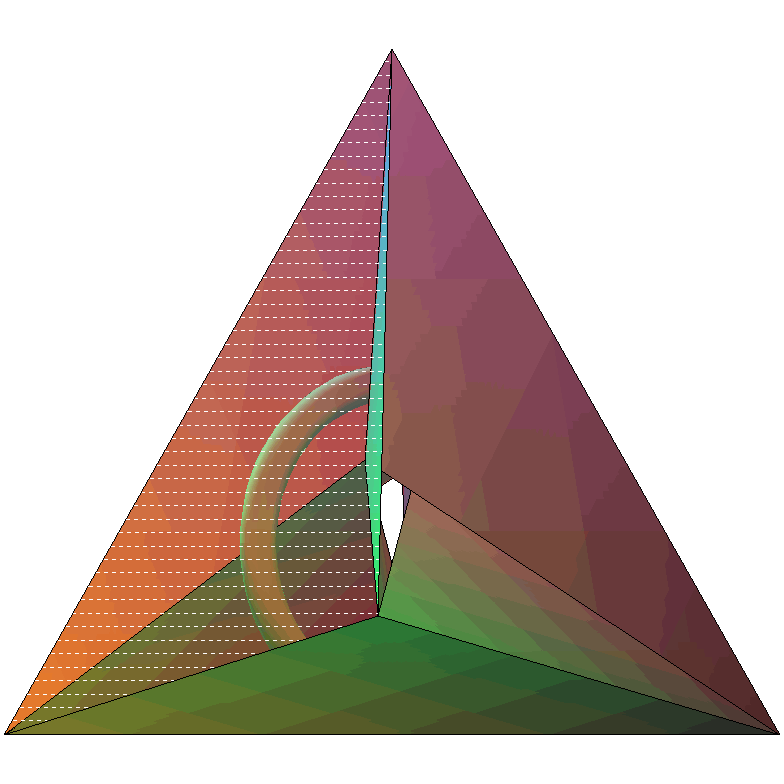
La vue de droite ci-dessus montre le "trou".
Remarques :
- son existence prouve a posteriori
que le graphe complet à 7 sommets peut être tracé sans
croisement sur le tore.
- le polyèdre est combinatoirement
régulier,
en ce sens que toutes les faces ont le même nombre d'arêtes
(3) et tous les sommets sont de même degré (6), mais les faces
ne sont pas géométriquement régulières
(non équilatérales).
- les sommets étant tous de
degré pair, le polyèdre est coloriable en deux couleurs.
- les 14 faces fournissent 14 groupes
de 3 objets parmi 7 tels que toute paire d'objets appartient exactement
à deux des 14 groupes de 3. Si l'on ne prend que les 7 faces coloriées
de l'une des deux couleurs, on obtient 7 groupes de 3 objets parmi 7 tels
que toute paire d'objets appartient exactement un des 7 groupes.
Concrètement, 7 personnes peuvent sortir par trinômes
chaque jour de la semaine, de sorte que chacun des 21 binômes possibles
sort exactement une fois (chaque personne sortira donc exactement 3 fois
et sera sortie avec chacune des 6 autres personnes).
Si F, S, A sont les nombres de faces, de sommets,
et d'arêtes d'un polyèdre à faces triangulaires de
genre n dont tous les couples de sommets sont reliés par
une arête, on a les relations ,
dont on tire
; n = 0 donne S = 4 et la seule solution est le tétraèdre,
n
=1 donne S = 7 ce qui explique pourquoi le polyèdre de Csazar
possède 7 sommets. La valeur suivante de n qui fournit un
S
entier est n = 6 qui donne S = 12, mais il n'a pas encore
été trouvé de polyèdre à 12 sommets
et 6 trous dont chaque sommet est relié aux 11 autres.
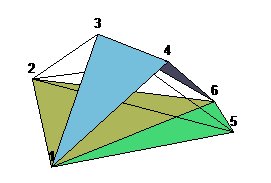
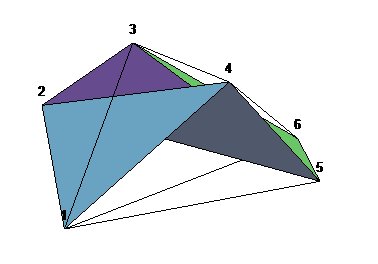
Construction :
 |
 |
 |
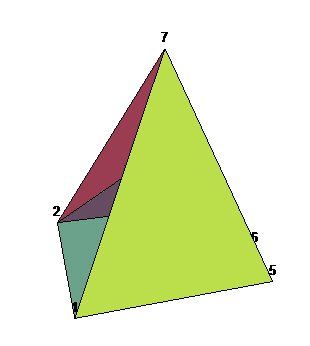 |
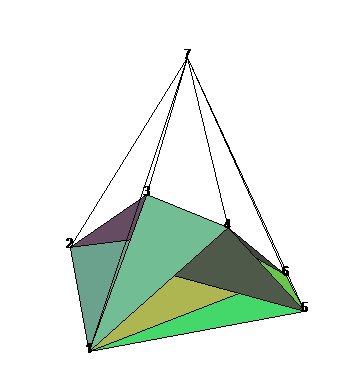
| 4 faces associées aux 6 premiers sommets. | 4 autres faces associées à ces sommets (124,245,253,356) | 8 faces de base. Il reste 6 arêtes libres qui seront reliées au septième sommet. | Les 14 faces. |
| Coordonnées des sommets proposées par Jean Lefort :
S1:=[6,6,0]: S2:=[6,-6,2]: S3:=[2,-3,6]: S4:=[-2,3,6]: S5:=[-6,6,2]: S6:=[-6,-6,0]:S7:=[0,0,15]: 2 faces du bas : F1:=[S1,S2,S6]:F2:=[S1,S5,S6]: 6 faces intermédiaires :F3:=[S1,S2,S4]: F4:=[S3,S4,S6]: F5:=[S3,S5,S6]: F6:=[S1,S3,S4]: F7:=[S2,S3,S5]: F8:=[S2,S4,S5]: 6 faces sommitales : F9:=[S2,S3,S7]: F10:=[S4,S5,S7]: F11:=[S4,S6,S7]:F12:=[S2,S6,S7]:F13:=[S1,S5,S7]:F14:=[S1,S3,S7]: |
Le polyèdre de Szilassi est un dual (combinatoire) du polyèdre de Csaszar.

Anaglyphe du polyèdre de Csaszar réalisé par Alain Esculier (à regarder avec des lunettes rouge à gauche et cyan à droite)
| polyèdre suivant | polyèdre précédent | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL
2015