polyèdre suivant polyèdre précédent courbes 2D courbes 3D surfaces fractals polyèdres

POLYÈDRE
Polyhedron, Polyeder


Premiers "polyèdres" : les boules de pierre gravées du néolithique ?
Du grec polus "plusieurs", hedra, "siège", "base" (donc "face").

Un polyèdre de l'espace euclidien à 3 dimensions E3 est un ensemble fini non vide de polygones (les faces du polyèdre) situés dans des plans de E3, les côtés et sommets de ces faces étant appelés les arêtes et sommets du polyèdre, tels que :
    1) chaque côté de chaque face coïncide avec un côté d'une seule autre face, non coplanaire avec la première.
    2) (condition de connexité) deux faces sont toujours reliées par une suite de faces, chaque face ayant une arête commune avec la suivante.
    3) (condition de non croisement) deux faces n'ont aucun point intérieur en commun.

REM : La condition 2) peut s'énoncer plus savamment en disant que le graphe dont les sommets sont les faces du polyèdre, deux sommets étant reliés par une arête si les faces correspondantes sont contiguës est connexe. Si l'on donnait seulement la condition que le graphe qui a même sommets et arêtes que le polyèdre est connexe, alors deux tétraèdres opposés par un sommet constitueraient un polyèdre !

Cette définition, qui exclut par exemple les polyèdres dits étoilés, admet diverses généralisations à voir sur la page des polyèdres généralisés.

NUMÉRATION

Un polyèdre possède au moins 4 sommets, 6 arêtes et 4 faces.

On classe les polyèdres suivant leur nombre de faces, appelé l'ordre du polyèdre, en utilisant les suffixes grecs suivants :
 
      4 5 6 7 8 9 10
      tétra penta hexa hepta octa ennéa
ou nona		 déca

 
11 12 13 14 15 16 17 18 19 20
hendéca ou
undéca		 dodéca tridéca tétradéca  le suffixe ...
...ci-dessus..
 plus déca   ...  ... icosa

 
21 22 23 24 25 26 27 28 29 30
icosiéna icosidi icositri icositétra icosi plus le...  ...suffixe.... ...ci-dessus  ...  ... triaconta

 
31 33   40 50 60 70 80 90 100 1000 10000
triacontaéna triacontatri etc. tétraconta pentaconta hexaconta heptaconta octaconta ennéaconta hecta chilia myria

Le nombre d'arêtes qui aboutissent à un sommet est le degré (ou valence) du sommet, toujours 3.

Le code de Schläfli d'un sommet est une suite des ordres des faces aboutissant à ce sommet ; par exemple 33.4.3.5 signifie qu'au sommet aboutissent, dans cet ordre, trois triangles, puis un quadrilatère, un triangle et enfin un pentagone.
Le code de Schläfli d'une face est une suite des degrés des sommets de cette face ; par exemple 33.4.3.5 signifie que les sommets de la face  sont, dans cet ordre, de degrés 3, 3, 3, 4, 3, 5.

La surface du polyèdre est la réunion des faces pleines ; c'est une surface connexe compacte plongée dans E3 donc homéomorphe au tore à n trous ; le nombre n est le genre du polyèdre, et dans le cas n = 0, le polyèdre est dit simple, ou simplement connexe (attention : une autre définition en conflit avec celle-ci dit qu'un polyèdre simple est un polyèdre dont les sommets sont de degré 3). Les nombres S de sommets, A d'arêtes et F de faces d'un polyèdre sont reliés par la relation d'Euler-Poincaré : S + F = A + 2 – 2n.
 
Exemple de polyèdre torique, de genre 1 : S = 9, F = 9, A = 18 = S + F.
C'est, à équivalence près, le polyèdre non simple d'ordre minimum.
La première étape de l'éponge de Sierpinski n'est pas un polyèdre au sens ci-dessus : les faces externes, percées d'un trou, ne sont pas des polygones. Mais si on les décompose et les déforme en créant 4 faces non coplanaires, comme l'indiquent les pointillés ci-contre, on obtient un polyèdre de genre 5 : 
S = 40, F = 48, A = 96 = S +F + 25 – 2.

La CNS pour qu'il existe un polyèdre simple ayant S sommets, A arêtes et F faces est donnée par la conjonction des 3 conditions (théorème de Steinitz) :
    • la relation d'Euler : S + F = A + 2
    • S 4
    • 2A 3.max (S, F) ;
on peut ainsi montrer qu'il n'existe pas de polyèdre simple ayant 7 arêtes.
 

Le polyèdre plein est la réunion de sa surface et des points "intérieurs" à cette surface, c'est-à-dire ceux à partir desquels toute courbe continue allant à l'infini rencontre la surface.

CONVEXITÉ
 
Un polyèdre est dit convexe si le polyèdre plein est convexe ; les faces en sont alors des polygones convexes.

Par contre, un polyèdre, même simple, à faces convexes, n'est pas forgément convexe.

Polyèdre simple non convexe à faces convexes.

Un polyèdre convexe est simple et le polyèdre plein est alors l'enveloppe convexe des sommets, ainsi que l'intersection de demi-espaces fermés définis par les faces. Réciproquement, toute enveloppe convexe d'un nombre fini de points et toute intersection d'un nombre fini de demi-espaces fermés qui est bornée est un polyèdre plein convexe (théorème de Minkowski).

Tout point intérieur à un polyèdre convexe se projette orthogonalement sur une face au moins ! En effet, on peut fixer ce point intérieur, mettre des masses aux sommets de sorte que ce point soit le centre de gravité du système obtenu, et ensuite dire que si ce point ne se projetait sur aucune face, alors, quelle que soit la face sur laquelle on pose le système il basculerait, ce qui serait absurde.
 
 
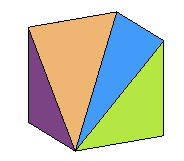
La donnée de ses sommets définit entièrement un polyèdre convexe ; le contre-exemple ci-contre montre que c'est faux si on enlève la condition de convexité, même pour des polyèdres sans trou.
Bien qu'ayant les mêmes sommets, ces deux polyèdres ne sont pas équivalents

ÉQUIVALENCE, SIMILITUDE,  ISOMÉTRIE

Deux polyèdres sont dits (combinatoirement) équivalents ou avoir la même combinatoire, s'il existe une bijection entre les sommets, conservant les arêtes et les faces. Une classe d'équivalence est un type de polyèdre.

Tout polyèdre simple est équivalent à un polyèdre convexe.
 
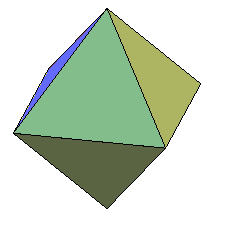
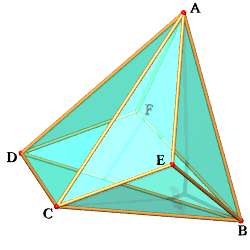
Avoir le même nombre de faces et de sommets (donc d'arêtes) ne suffit pas à avoir la même combinatoire.
Par exemple, ces deux polyèdres ont 8 faces et 6 sommets, mais l'octaèdre à gauche a tous ses sommets de degré 4, tandis que le polyèdre de droite a 2 sommets de degré 5 (A et B), 2 sommets de degré 4 (C et D), et 2 sommets de degré 3 (E et F).

Deux polyèdres sont dits isométriques (ou congruents) (resp. semblables) s'il existe une isométrie (resp. une similitude) de l'espace conservant les faces. Isométriques implique semblables, qui implique équivalents, mais les réciproques sont fausses. On confond en général deux polyèdres semblables.
 
Contrairement à ce que pensait Euclide, deux polyèdres, même convexes, ayant des faces isométriques deux à deux ne sont pas forcément isométriques. Un contre-exemple est fourni par le cuboctaèdre et le pseudo-cubocataèdre.
Par contre deux polyèdres convexes équivalents ayant des faces correspondantes isométriques sont isométriques (théorème de Cauchy).
Ce dernier théorème est lui-même faux pour des polyèdres non convexes, voir la page sur les polyèdres flexibles.

Ces deux polyèdres ont des faces isométriques 
mais ne sont pas isométriques (ils ne sont même pas équivalents).

SQUELETTE, GRAPHE, PATRON
 

Le squelette du polyèdre est la réunion de ses arêtes pleines. 
La donnée du squelette d'un polyèdre définit donc ses sommets et ses arêtes, mais pas forcément ses faces, comme le montre le contre-exemple ci-contre.
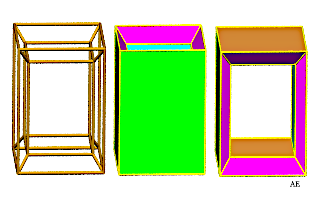Ces deux polyèdres ont le même squelette, mais pas les mêmes faces.
Ils sont cependant équivalents.

Un graphe non orienté simple est dit associé à un polyèdre s'il existe une bijection entre les sommets du graphe et ceux du polyèdre, préservant les arêtes, par exemple le graphe défini par le squelette du polyèdre. Deux polyèdres équivalents ont des graphes associés isomorphes, mais la réciproque est fausse (voir ci-contre un contre-exemple dû à Guy Valette). Dans le cas d'un polyèdre simple, on appelle diagramme de Schlegel toute représentation plane d'un graphe associé, avec des arêtes rectilignes sans croisement. On obtient un tel diagramme dans le cas d'un polyèdre inscriptible par projection stéréographique sur un plan tangent à la sphère en un point autre qu'un sommet.

Les deux polyèdres ci-dessus ont même squelette (donc même graphe associé) mais ne sont pas équivalents.
Celui de gauche est de genre 1 : S = 24, A = 48, F = 6+6+6+6 = 24.
Celui de droite est de genre 2 : S = 24, A = 48, F = 3+3+4+4+4+4=22..

Voir aussi un cas triple pour des polyèdres étoilés

Un graphe non orienté est associé à un polyèdre simple si et seulement s'il remplit les conditions suivantes (autre théorème de Steinitz) :
    - posséder au moins 4 sommets
    - être connexe et rester connexe quand on retire 2 sommets quelconques
    - être représentable sans croisement dans le plan, autrement dit être "planaire".

Un patron d'un polyèdre est une réunion de polygones pleins dans un plan, isométriques aux faces du polyèdre, ne se chevauchant pas, chaque polygone étant attaché à exactement un autre par une arête et permettant par pliage de reconstituer la surface du polyèdre.
Attention, le patron peut ne pas être caractéristique du polyèdre : Voir ici un exemple de patron qui conduit à deux polyèdres distincts.

INSCRIPTIBILITÉ, CIRCONSCRIPTIBILITÉ

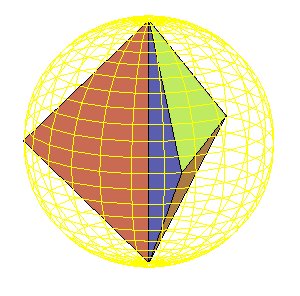Un polyèdre est dit inscriptible (ou inscrit) si ses sommets sont situés sur une même sphère ; la figure ci-contre montre qu'il n'est alors pas forcément convexe. Par projection conique de centre le centre de la sphère, on obtient dans le cas convexe un pavage de la sphère par des polygones sphériques (par contre, un pavage sphérique ne fournit pas forcément un polyèdre inscriptible, sauf si les sommets de chaque polygone sphérique sont coplanaires).
 

Un exemple de polyèdre convexe non inscriptible est le cube tronqué en un sommet, mais il est équivalent à un polyèdre inscriptible. Un polyèdre convexe n'est pas forcément équivalent à un polyèdre inscriptible ; voir ici un article donnant une CNS pour qu'un polyèdre convexe soit équivalent à un polyèdre inscriptible.
Un polyèdre est dit circonscriptible (ou circonscrit), si ses faces prolongées sont tangentes à une même sphère.
Le dual (P*) d'un polyèdre inscriptible (P) obtenu par polarité par rapport à la sphère circonscrite à (P) est circonscrit à cette sphère (mais attention, ce dual peut être un polyèdre étoilé), et réciproquement, le dual (P*) d'un polyèdre circonscriptible (P) obtenu par polarité par rapport à la sphère inscrite dans (P) est inscrit dans cette sphère (mais là aussi, ce dual peut être un polyèdre étoilé).

VOIR AUSSI

Site de J.J. Dupas : cm2.ens.fr

Site très complet sur les polyèdres : www.polyhedra-world.nc

Méthode pour tracer les faces des polyèdres par Alain Esculier

Logiciel pour tracer des polyèdres : www.peda.com/poly/download.html

Site de G. Tulloue : phyanim.sciences.univ-nantes.fr/Polyedres/index.php

The Euler-Poincaré Formula : www.cs.mtu.edu/~shene/COURSES/cs3621/NOTES/model/euler.html

Site du sculpteur Antoine Walter : www.delcaflor.net/espace/polyedres/index.html

Site de George Hart : www.georgehart.com/virtual-polyhedra/vp.html

Polyhedra Collection : bulatov.org/polyhedra/

Articles de Jorge Rezende : gfm.cii.fc.ul.pt/Members/JR.en.html
 
 


polyèdre suivant polyèdre précédent courbes 2D courbes 3D surfaces fractals polyèdres

© Robert FERRÉOL 2023