Le tamis de Sierpinski a été étudié par Sierpinski en 1915, mais le pentagone de Dürer date de 1500... Quand au mot fractal, il n'a été créé par Mandelbrot qu'en 1975 ! Waclaw Sierpinski (1882-1969) : mathématicien polonais. Admirez une éponge de Sierpinski en tickets de tram !

Le principe général de construction d'un fractal de Sierpinski est le suivant. On part d'un objet contenant un certain nombre p de parties isométriques entre elles, qui lui sont homothétiques et qui ne se coupent que suivant leurs frontières ; on évide dans l'objet le complémentaire de la réunion des parties homothétiques et on recommence l'opération à l'infini dans chacun des p objets homothétiques.
L'objet limite n'est alors autre que l'attracteur des p homothéties transformant l'objet de départ en ses parties homothétiques.

En dimension 1, le fractal de Sierpinski le plus simple est l'ensemble de Cantor.

En dimension 2, les 4 fractals les plus célèbres sont le triangle (ou tamis), le carré (ou tapis, carpette, napperon),  le pentagone et l'hexagone de Sierpinski.

    - pour le carré (en anglais "Sierpinski carpet"), l'objet de départ est un carré plein de côté a et les parties homothétiques les 8 carrés de coté a/3 accolés à sa frontière :

Le tapis de Sierpinski est donc l'attracteur de 8 homothéties de rapport 1/3 centrées aux sommets et aux milieux des côtés d'un carré : dimension fractale = » 1,9 ; en voir une courbe remplissante ici.
Rem : Les diagonales et médianes du tapis de Sierpinski sont des ensembles de Cantor.

Voir de nombreuses variantes du carré de Sierpinski sur la page correspondante.

    - voici le pentagone de Sierpinski, digne des dentelles flamandes :
 

C'est l'attracteur de 5 homothéties de rapport  centrées aux sommets d'un pentagone régulier : dimension fractale = .

Si l'on part du pentagone régulier étoilé, les figures obtenues sont également très élégantes :

    - et le tout aussi dentelé hexagone de Sierpinski :
 

C'est l'attracteur de 6 homothéties de rapport 1/3 centrées aux sommets d'un hexagone régulier : dimension fractale = 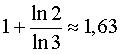. Chacun aura remarqué que la partie évidée centrale est un flocon de Koch ; les six côtés sont des courbes de Koch.

Ces divers fractals peuvent bien sur se généraliser à un polygone régulier convexe quelconque ; le polygone de Sierpinski d'ordre n  est l'attracteur de n homothéties de rapport  centrées au sommet d'un polygone régulier convexe d'ordre n. Ce rapport est choisi de sorte que les n images du polygone plein de départ soient juste jointives. Attention, cette généralisation redonne tous les cas ci-dessus, sauf le cas n = 4 (où elle donne le carré plein) ; remarquons que pour n compris entre 5 et 8, le rapport se simplifie en .
Voici par exemple l'élégant octogone de Sierpinski :
 
 
 

Ci contre un programme à coller dans Maple pour tracer ces polygones :

sierpinski:=proc(x,y,a,n,p)                                                                b:=1/2/evalf(sum(cos(2*q*Pi/n),q=0..floor(n/4))):   if p=0 then  polygonplot([seq([x+a*cos(k*Pi*2/n),y+a*sin(k*Pi*2/n)],k=1..n)])  else seq(sierpinski(x+(1-b)*a*cos(k*Pi*2/n),y+(1-b)*a*sin(k*Pi*2/n),a*b,n,p-1), k=1..n) fi end:  display(sierpinski(0,0,1,6,3),color=red,style=patchnogrid,axes=none,scaling=constrained);

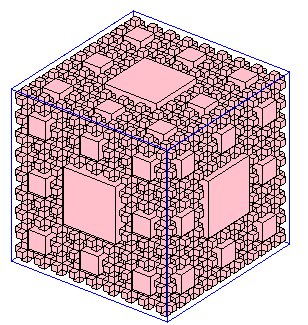
En dimension 3, le fractal de Sierpinski le plus célèbre, version 3D du tapis, est l'éponge de Menger découverte en 1925 (Karl Menger : 1902 - 1985 : mathématicien américain), attracteur de 20 homothéties de rapport 1/3 centrées aux sommets et aux milieux des arêtes d'un cube, de dimension fractale .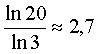

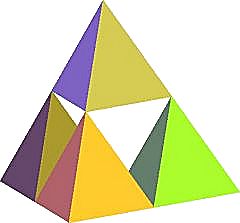
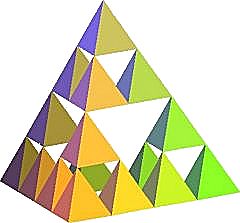
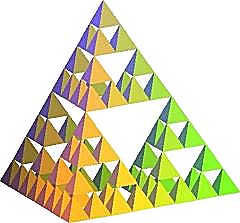
On peut aussi construire des objets similaires à partir des 3 autres polyèdres réguliers :

Voir cette page donnant des exemples de fractals de Sierpinski 3D.
 

Complémentaire de l'éponge de Menger

Coupe transversale d'une éponge de Menger faisant apparaïtre des hexagones...

Variante, dûe à Nicolas Douillet, basée sur un partage du cube en 5^3 = 125 parties cubiques, en en conservant 57 à chaque nouvelle itération.

 

fractal suivant

fractal précédent

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL 2022