Courbe de Koch

Courbe étudiée par Koch en 1904.
Niels Fabian Helge von Koch (1870-1924) : mathématicien suédois.
Animations à voir absolument sur aesculier.fr/fichiersMaple/koch/koch.html

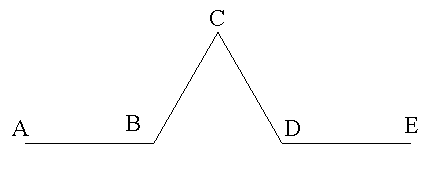
La courbe de Koch est l'attracteur dans le plan des 4 similitudes de rapport 1/3 transformant (A, E) respectivement en (A, B), (B, C), (C, D) et (D, E) (avec BD = AB) (voir figure)
Sa dimension fractale est donc

Voici la suite des compacts convergeant vers cette courbe, en partant de [AE] :

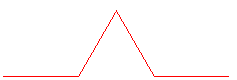
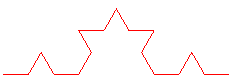
Elle a été introduite par von Koch comme exemple de "courbe continue sans tangente, obtenue par une construction géométrique élémentaire"; cette courbe présente également le paradoxe d'être de longueur infinie bien que bornée et sans point asymptote. La longueur de la courbe approchée à l'étape est la longueur de la base multipliée par (4/3)ⁿ : pour une base de 1 cm, la courbe à l'étape 40 est déjà longue de 1 km ! Mais ceci n'est que théorique, puisqu'on ne peut guerre dépasser l'étape 5 à cause de l'épaisseur du trait.

Remarquons que la base de la courbe de koch est un ensemble de Cantor.

Lorsqu'on accole trois courbe de Koch aux sommets d'un triangle équilatéral on obtient une élégante figure à symétrie hexagonale dénommée flocon de Koch (ou île de Koch) - en anglais : Koch snowflake or Koch island.

Construction animée du flocon de Koch, d'après une idée de Benoit Rittaud, réalisée par Alain Esculier.

Bien que la longueur de la frontière du flocon soit infinie (à chaque étape, la longueur est multipliée par 4/3), l'aire du flocon est finie et vaut les 8/5 de celle du triangle.

Ces flocons peuvent paver le plan :

Lorsqu'on met les courbes à l'intérieur du triangle, on obtient le flocon inversé, occasion d'un délicieux jeu de mots en anglais : the Koch flowsnake.

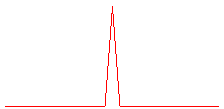
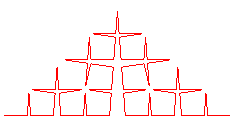
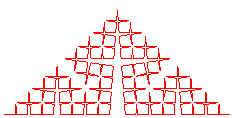
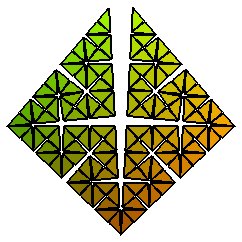
La courbe de Koch a d'innombrables variantes, dont la plus naturelle est de prendre des homothéties de rapport k entre 1/4 et 1/2 (tout en conservant la ligne brisée de 4 segments égaux). Cette courbe pour k aux environs de 0,4 fait penser aux branchies du poumon :

Lorsqu'on arrive au cas limite k = 1/2, on obtient une courbe de dimension fractale 2, connue sous le nom de courbe de Cesàro (1905), et remplissant entièrement un triangle rectangle isocèle :

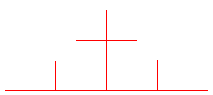
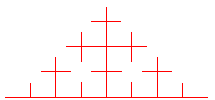
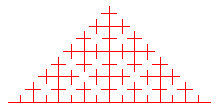
Dans ces figures, nous avons raccourci les extrémités des segments pour éviter qu'ils ne se rejoignent.

Quatre de ces courbes forment alors une courbe remplissant un carré, courbe qui ne se trouve être autre, à la limite, que la courbe de Sierpinski.

Pour , on obtient l'élégant flocon carré :

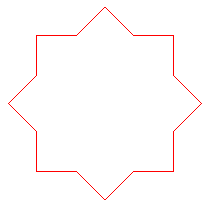
ou la variante en croix :

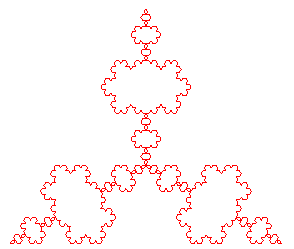
Dans la figure ci-dessous, nous avons modifié l'algorithme classique en positionnant aléatoirement le triangle équilatéral d'un côté ou de l'autre du segment. On obtient une figure ressemblant fortement à une côte rocheuse comme celle de la Bretagne (étape 5). Cette courbe a manifestement la même dimension fractale que la courbe de Koch, mais n'est plus auto-similaire au sens strict !

Voir aussi la courbe de Koch quadratique.

Même les extra-terrestres connaissent le flocon de Koch !

fractal suivant fractal précédent courbes 2D courbes 3D surfaces fractals polyèdres