Courbe de Sierpinski

COURBE DE SIERPINSKI
Sierpinski's curve, Sierpinskische Kurve

Courbe étudiée par Sierpinski en 1915 (W. Sierpinski, Sur une courbe dont tout point est un point de ramification, C. R. Acad. Sci. Paris 160 (1915) 302-305).
Waclaw Sierpinski (1882-1969) : mathématicien polonais.
Article : Rapport avec un kolam indien.
Voir aussi cette page d'Alain Esculier.

La courbe de Sierpinski est une courbe remplissant un carré, courbe limite des constructions ci-dessous :

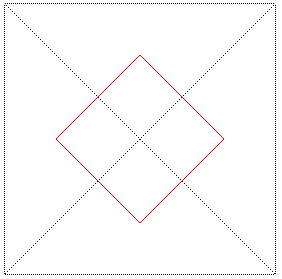
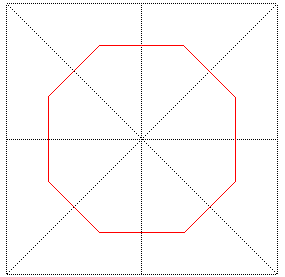
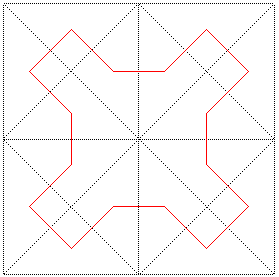
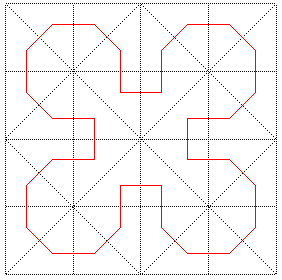
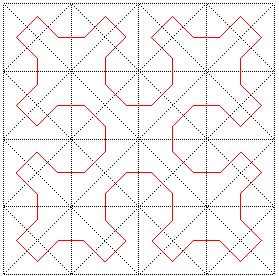
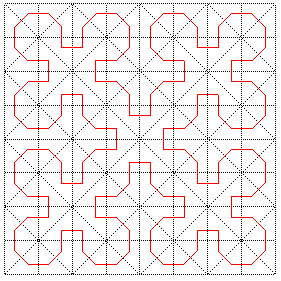
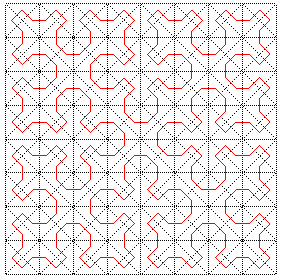
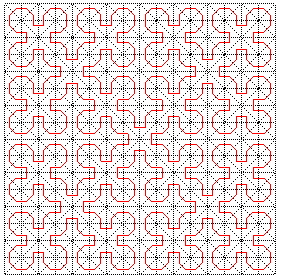
Cette construction, exploitant le fait qu'un triangle rectangle isocèle se partage en deux triangles rectangles isocèles identiques, est distincte de celles de Peano (un carré partagé en 9 carrés) ou de Hilbert (un carré partagé en 4 carrés).
Le point que nous avons choisi dans chaque triangle est le centre du cercle inscrit (de sorte que tous les segments ont la même longueur), mais le point choisi n'a en fait pas d'influence sur la courbe finale.

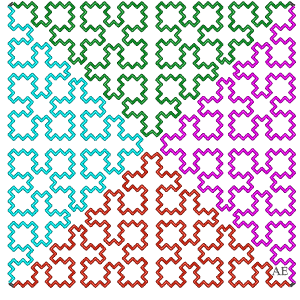
Les figures suivantes montrent le lien entre la courbe de Sierpinski et la réunion de 4 courbes de Cesàro :

Remplissage du carré par 4 courbes de Cesàro

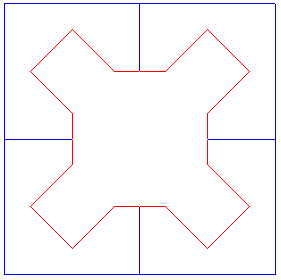
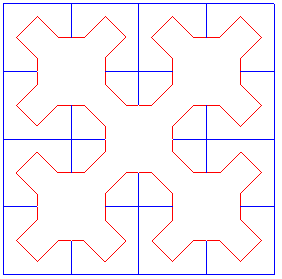
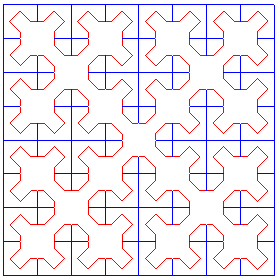
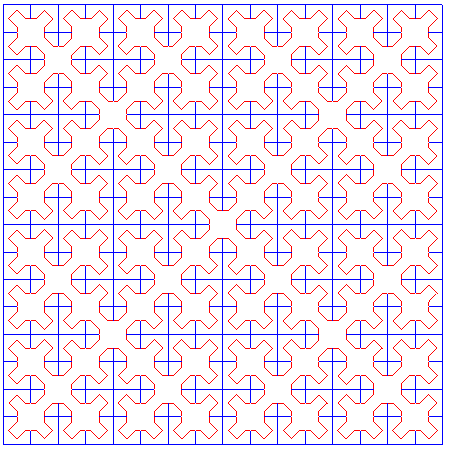
Les courbes de Sierpinski approchées se distinguent des courbes de Cesàro par le fait qu'elles sont sans point doubles et particulièrement esthétiques, mais les courbes limites sont les mêmes !

Paradoxe : le domaine fermé englobé par la courbe de Sierpinski tend vers le carré ouvert entier bien que son aire ne tende que vers une fraction égale à de l'aire de celui-ci !

Formules pour la longueur et l'aire (a est le côté du carré) : L(0) = 8*a*(sqrt(2)-1) ; L(n)=2*L(n-1); S(0)=(5-3*sqrt(2))/2*a^2 ; S(n)=S(n-1)+(rac(2)-1)/2/4^n*a^2.

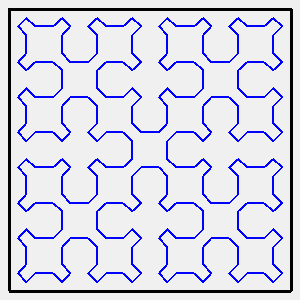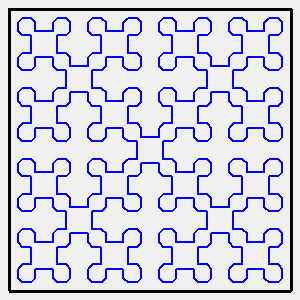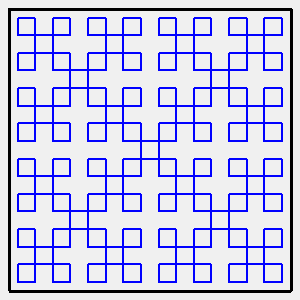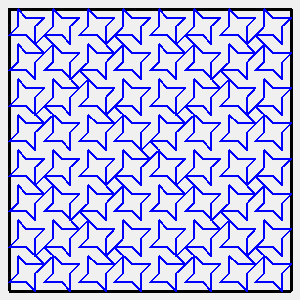
A gauche, variante avec uniquement des angles droits, que l'on trouve sous le nom de "square curve".
A droite, animation montrant la déformation vers la variante suivante.

Si l'on joint directement les centres des carrés, on obtient la courbe ci contre, que l'on a d'ailleurs tendance à parcourir différemment de celle de Sierpinski, comme indiqué sur la figure de droite.

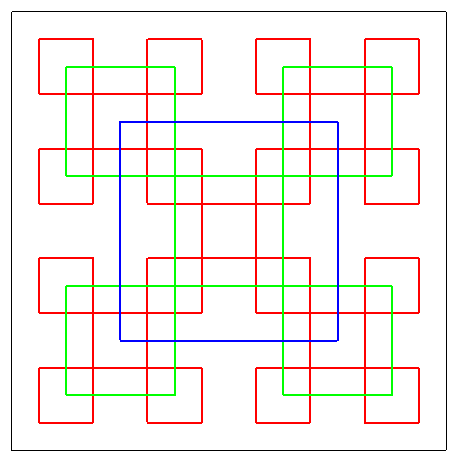
Cette courbe peut être obtenue à partir du carré central de côté moitié du grand carré, en appliquant à chaque étape les 4 homothéties de rapport 1/2 centrées aux sommets du carré, et en ajoutant un petit carré central.
L'attracteur des 4 homothéties est bien le carré entier.
A l'étape n, il y a (4.4^n-1)/3 petits carrés et l'aire totale tend vers les 12/48 = 1/4 de l'aire du grand carré.
Programme maple réalisé par Alain Esculier :
Lhomo := (centre,k,Liste) ->
if type(evalf(Liste[1,1]),numeric) then map(u -> expand(centre+(u-centre)*k),Liste) else map(u -> Lhomo(centre,k,u),Liste) fi :
sierp := proc (n)
local L,i,a,centres,base;
a:=1/2:base := [[-a, -a],[a, -a],[a, a],[-a, a]]:
L := [base]; centres := [[-1, -1],[1, -1],[1, 1],[-1, 1]];
for i to n do L := [seq(op(Lhomo(centres[i], a, L)), i = 1 .. nops(centres)), expand(a^i*base)] od:
end:
display([polygonplot([[-1, -1], [1, -1], [1, 1], [-1, 1]]),polygonplot(sierp(5), color=red)], style = line, axes = none);

Ne pas confondre cette courbe avec la courbe du triangle de Sierpinski.

Que diriez vous d'un carrelage de Sierpinski, à deux types de carreaux ?

Figure kolam traditionnelle indienne suivant le même principe

fractal suivant fractal précédent courbes 2D courbes 3D surfaces fractals polyèdres