Polyèdres étudiés par Johnson en 1966 et Zalgaller en 1967. Voir aussi : mathworld.wolfram.com/JohnsonSolid.html www.polyhedra-world.nc/Johnson.htm www.georgehart.com/virtual-polyhedra/johnson-index.html Liste de polyèdres proches de polyèdres CFR Images de cette page réalisées avec le logiciel poly.

Un polyèdre convexe à faces régulières (en abrégé : CFR) est, comme son nom l'indique, un polyèdre convexe dont toutes les faces sont des polygones réguliers.

Hormis les polyèdres réguliers ou semi-réguliers, il n'existe qu'un nombre fini de polyèdres CFR, appelés polyèdres de Johnson. Ce n'est qu'en 1967 que la liste exacte de ces polyèdres, au nombre de 92, a été établie et démontrée, avec une désignation du type J_k (k = 1..92) et une nomenclature permettant de retrouver leur construction. Seuls 17 de ces 92 polyèdres (notés S₁ à S₁₇ ci-dessous - S comme "Simple") ne sont pas somme de polyèdres CFR strictement plus petits.

Voici la liste de tous les polyèdres CFR (les noms indiqués sont les traductions des noms anglais donnés par Zalgaller, suivies d'autres appellations françaises, certaines dues à Guy Valette):

1) Une infinité de prismes à faces régulières P₃, P₄ (le cube),P₅, .... qui sont semi-réguliers.

2) Une infinité d'antiprismes à faces régulières A₃(l'octaèdre), A₄, ....qui sont semi-réguliers.

3) Les 3 pyramides à faces régulières Py₃(le tétraèdre), Py₄ (notée J₁ , ou S₁) et Py₅ (J₂ ou S₂), qui sont inscriptibles à faces régulières (IFR).

4) 3 "coupoles" C₆ (J₃ ou S₃), C₈ (J₄ ou S₄) et C₁₀ (J₅ ou S₅), qui sont IFR :
 

Composition "atomique"	Vue	patron	Nom	particularité	Jk	F	A	S
C6			coupole hexagonale	IFR	J3	8	15	9
C8			coupole octogonale	IFR	J4	10	20	12
C10			coupole décagonale	IFR	J5	12	25	15

4) 1 "rotonde" R₁₀ (J₆ et S₆) , qui est IFR:
 

Composition "atomique"	vue	patron	Nom	particularité	Jk	F	A	S
R10			rotonde décagonale	IFR	J6	17	35	20

5) 55 polyèdres composés des précédents, dont 5 sont semi-réguliers :
 

Composition "atomique"	vue	patron	Nom	particularité	Jk	F	A	S
1. Py3P3			pyramide triangulaire allongée		J7	7	12	7
2. Py4P4			pyramide carrée allongée		J8	9	16	9
3. Py5P5			pyramide pentagonale allongée		J9	11	20	11
Py3A3			pyramide triangulaire gyro-allongée c'est un rhomboèdre.	raté ! deux triangles se raccordent en un losange, les faces ne sont plus régulières !
4. Py4A4			pyramide carrée gyro-allongée		J10	13	20	9
5. Py5A5			pyramide pentagonale gyro-allongée ou icosaèdre diminué	IFR	J11	16	25	11
6. Py32			bipyramide triangulaire	deltaèdre	J12	6	9	5
Py42  = A3			bipyramide carrée ou octaèdre	régulier		8	12	6
7. Py52			bipyramide pentagonale	deltaèdre	J13	10	15	7
8. Py3P3Py3			bipyramide triangulaire allongée Voir ce site.		J14	9	15	8
9. Py4P4Py4			bipyramide carrée allongée		J15	12	20	10
10. Py5P5Py5			bipyramide pentagonale allongée		J16	15	25	12
11. Py3A3Py3			bipyramide carrée gyro-allongée ou hexadécadeltaèdre	deltaèdre	J17	16	24	10
12. Py5A5Py5 ou S7Py53			bipyramide pentagonale gyro-allongée  ou icosaèdre	régulier		20	30	12
13. C6P6			coupole hexagonale allongée		J18	14	27	15
14. C8P8			coupole octogonale allongée		J19	9	16	9
15. C10P10			coupole décagonale allongée		J20	22	45	25
16. R10P10			rotonde décagonale allongée		J21	27	55	30
17. C6A6		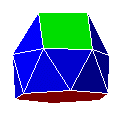	coupole hexagonale gyro-allongée		J22	20	33	15
18. C8A8		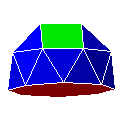	coupole octogonale gyro-allongée		J23	26	44	20
19. C10A10		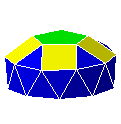	coupole décagonale gyro-allongée		J24	32	55	25
20. R10A10			rotonde décagonale gyro-allongée		J25	37	65	30
21. C62		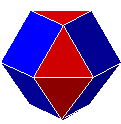	bicoupole hexagonale ou gyro-cuboctaèdre	IFR	J27	14	24	12
22. C82			bicoupole octogonale		J28	18	32	16
23. C102			bicoupole décagonale		J30	22	40	20
24. R102			birotonde décagonale ou gyro-icosidodécaèdre		J34	32	60	30
25. C10R10			coupole-rotonde décagonale		J32	27	50	25
26. C6C6		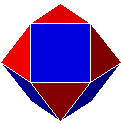	gyrobicoupole hexagonale ou cuboctaèdre	semi-régulier		14	24	12
27. C8C8			gyrobicoupole octogonale		J29	18	32	16
28. C10C10			gyrobicoupole décagonale		J31	22	40	20
29. R102			gyrobirotonde décagonale ou icosidodécaèdre	semi-régulier		32	60	30
30. C10R10		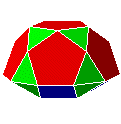	gyrocoupole-rotonde décagonale		J33	27	50	25
31. C6P6C6		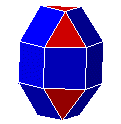	bicoupole hexagonale allongée		J35	20	36	18
32. C8P8C8		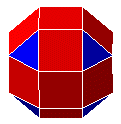	bicoupole octogonale allongée ou rhombicuboctaèdre	semi-régulier		26	48	24
33. C10P10C10			bicoupole décagonale allongée		J38	32	60	30
34. R10P10R10			birotonde décagonale allongée		J42	42	80	40
35. C10P10R10			coupole-rotonde décagonale allongée		J40	37	70	35
36. C6P6C6		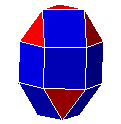	gyrobicoupole hexagonale allongée		J36	20	36	18
37. C8P8C8		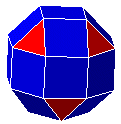	gyrobicoupole octogonale allongée ou gyro-rhombicuboctaèdre	IFR	J37	26	48	24
38. C10P10C10		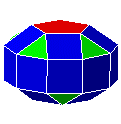	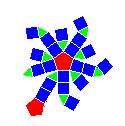gyrobicoupole décagonale allongée		J39	32	60	30
39. R10P10R10			gyrobirotonde décagonale allongée		J43	42	80	40
40. C6P6C6			gyrocoupole-rotonde décagonale allongée		J41	37	70	35
41. C6A6C6			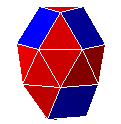bicoupole hexagonale gyro-allongée	2 versions chirales	J44	26	42	18
42. C8A8C8			bicoupole octogonale gyro-allongée	2 versions chirales	J45	34	56	24
43. C10A10C10			bicoupole décagonale gyro-allongée	2 versions chirales	J46	42	70	30
44. R10A10R10		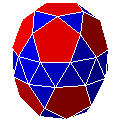	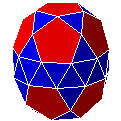birotonde décagonale gyro-allongée	2 versions chirales	J48	52	90	40
45. C10A10R10			coupole-rotonde decagonale gyro-allongée	2 versions chirales	J47	47	80	35
46. P32			gyrobifastigium ou gyro-biprisme triangulaire ou octaèdre biprismatique	polyèdre pavant l'espace	J26	8	14	6
47. P3Py4			prisme triangulaire augmenté		J49	8	13	7
48. P3Py42			prisme triangulaire biaugmenté		J50	11	17	8
49. P3Py43			prisme triangulaire triaugmenté ou tétradécadeltaèdre	deltaèdre	J51	14	21	9
50. P5Py4			prisme pentagonal augmenté		J52	10	19	11
51. P5Py42		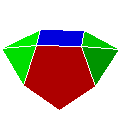	prisme pentagonal biaugmenté		J53	11	17	8
52. P6Py4		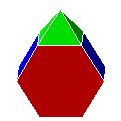	prisme hexagonal augmenté		J54	11	22	13
53. Py4P6Py4			prisme hexagonal parabiaugmenté		J55	14	26	14
54. P6Py42		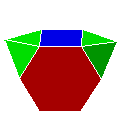	prisme hexagonal métabiaugmenté		J56	14	26	14
55. P6Py43		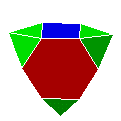	prisme hexagonal triaugmenté		J57	17	30	15

6) 5 polyèdres apparentés au dodécaèdre :
 

Composition "atomique"	vue	patron	Nom	particularité	Jk	F	A	S
D5		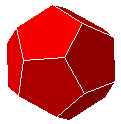	dodécaèdre	régulier		12	30	10
D5Py5		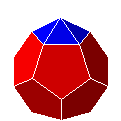	dodécaèdre augmenté		J58	16	35	21
Py5D5Py5		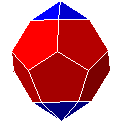	dodécaèdre parabiaugmenté		J59	20	40	22
D5Py52		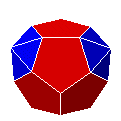	dodécaèdre métabiaugmenté		J60	20	40	22
D5Py53		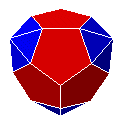	dodécaèdre triaugmenté		J61	24	45	23

7) 3 polyèdres apparentés à l'icosaèdre :
 

Composition "atomique"	vue	patron	Nom	particularité	Jk	F	A	S
S7Py5			icosaèdre métabidiminué	IFR	J62	12	20	10
S7			icosaèdre tridiminué	IFR	J63	8	15	9
S7Py3			icosaèdre tridiminué augmenté		J64	10	18	10

8) 2 polyèdres apparentés au tétraèdre tronqué
 

Composition "atomique"	vue	patron	Nom	particularité	Jk	F	A	S
Tt		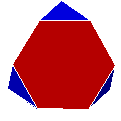	tétraèdre tronqué	semi-régulier		8	18	12
TtC6		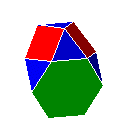	tétraèdre tronqué augmenté		J65	14	27	14

9) 3 polyèdres apparentés au cube tronqué
 

Composition "atomique"	vue	patron	Nom	particularité	Jk	F	A	S
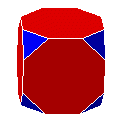
Ct			cube tronqué	semi-régulier		14	36	24
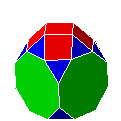
CtC8			cube tronqué augmenté		J66	22	48	28
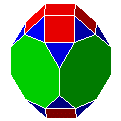
C8CtC8			cube tronqué biaugmenté		J67	30	60	32

10) 5 polyèdres apparentés au dodécaèdre tronqué :
 

Composition "atomique"	vue	patron	Nom	particularité	Jk	F	A	S
Dt		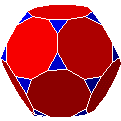	dodécaèdre tronqué	semi-régulier		32	90	60
DtC10		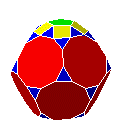	dodécaèdre tronqué augmenté		J68	42	105	65
C10DtC10		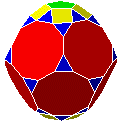	dodécaèdre tronqué parabiaugmenté		J69	52	120	70
DtC102		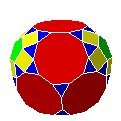	dodécaèdre tronqué métabiaugmenté		J70	52	120	70
DtC103			dodécaèdre tronqué triaugmenté		J71	62	135	75

11) 13 polyèdres apparentés au rhombicosidodécaèdre :
 

Composition "atomique"	vue	patron	Nom	particularité	Jk	F	A	S
S8C102 ou S9C103			rhombicosidodécaèdre	semi-régulier		62	120	60
C10S8C10			gyro-rhombicosidodécaèdre ou rhombicosidodécaèdre circiné (ou remplacer "circiné" par "pivoté") une décacoupole a été pivotée d'un dixième de tour	IFR	J72	62	120	60
C10S8C10			parabigyro-rhombicosidodécaèdre rhombicosidodécaèdre parabicirciné deux décacoupoles opposées pivotées (en haut et en bas sur la figure)	IFR	J73	62	120	60
C102S9C10			métabigyro-rhombicosidodécaèdre ou rhombicosidodécaèdre métabicirciné deux décacoupoles adjacentes pivotées (à gauche et à droite sur la figure)	IFR	J74	62	120	60
C103S9			trigyro-rhombicosidodécaèdre ou rhombicosidodécaèdre tricirciné trois décacoupoles  pivotées	IFR	J75	62	120	60
C10S8			rhombicosidodécaèdre diminué	IFR	J76	52	105	55
S8C10			paragyro-rhombicosidodécaèdre diminué (anticonstitutionnellement est battu...)  ou rhombicosidodécaèdre diminué paracirciné une décacoupole supprimée, la décacoupole opposée pivotée	IFR	J77	52	105	55
C10S9C10			métagyro-rhombicosidodécaèdre ou rhombicosidodécaèdre métacirciné une décacoupole supprimée, la décacoupole adjacente pivotée	IFR	J78	52	105	55
C102S9			bigyro-rhombicosidodécaèdre diminué ou rhombicosidodécaèdre diminué bicirciné une décacoupole supprimée, deux décacoupoles pivotées	IFR	J79	52	105	55
S8			rhombicosidodécaèdre parabidiminué deux décacoupoles opposées supprimées	IFR	J80	42	90	50
S9C10		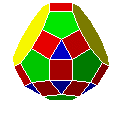	rhombicosidodécaèdre métabidiminué deux décacoupoles adjacentes supprimées	IFR	J81	42	90	50
C10S9		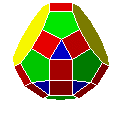	gyro-rhombicosidodécaèdre bidiminué ou rhombicosidodécaèdre bidiminué circiné	IFR	J82	42	90	50
S9		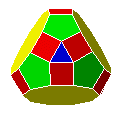	rhombicosidodécaèdre tridiminué	IFR	J83	32	75	45

12)  6 polyèdres semi-réguliers "secs".
 

vue	patron	Nom	particularité	F	A	S
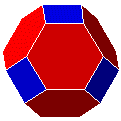		octaèdre tronqué	semi-régulier	14	36	24
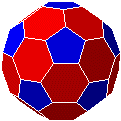		icosaèdre tronqué	semi-régulier	32	90	60
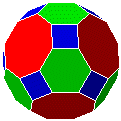		cuboctaèdre tronqué	semi-régulier	26	72	48
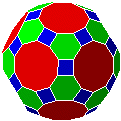		icosidodécaèdre tronqué	semi-régulier	62	180	120
		cube adouci	semi-régulier	38	60	24
		dodécaèdre adouci	semi-régulier	92	150	60

13)   9 polyèdres exotiques non apparentés aux précédents
 

Composition "atomique"	vue	patron	Nom	particularité	Jk	F	A	S
S10			disphénoïde adouci ou dodécadeltaèdre deux pyramides pentagonales flexées symétriques plus une "bouche" formée de deux triangles.	deltaèdre	J84	12	18	8
S11		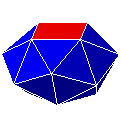	antiprisme carré adouci ou icosihexaèdre "antiprisme ventru" On remplace dans l'antiprisme carré (figure du bas) chaque arête joignant les deux carrés par deux triangles.		J85	26	40	16
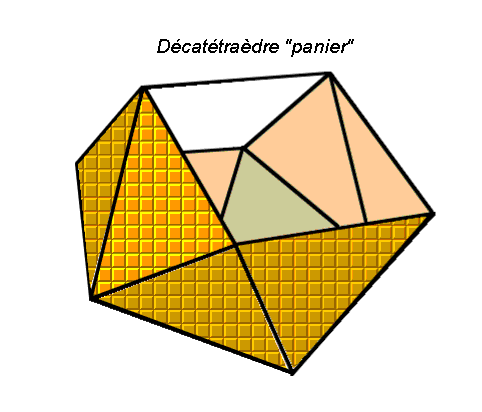
S12			sphéno-couronne ou décatétraèdre "panier" deux pyramides pentagonales flexées symétriques plus une "bouche" formée de deux triangles et deux carrés.		J86	14	22	10
S12Py4		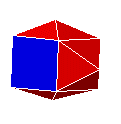	sphéno-couronne augmentée ou décatétraèdre "panier" augmenté		J87	17	26	11
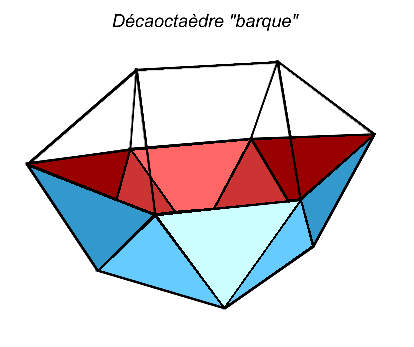
S13		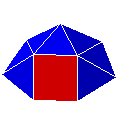	sphéno-mégacouronne ou décaoctaèdre "barque"		J88	18	28	12
S14		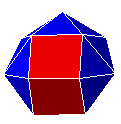	hébésphéno-mégacouronne ou icosiénaèdre de Johnson		J89	21	33	14
S17			disphénocingulum (cingulum = ceinture) ou icositétraèdre à deux tranchants		J90	24	38	16
S15			bilune-birotonde ou décatétraèdre à deux tranchants		J91	14	26	14
S16			hébésphéno-rotonde triangulaire ou icosaèdre de degré 4		J92	20	36	18

Notons qu'il existe une infinité de polyèdres à faces régulières, même simples, mais non supposés convexes. On peut par exemple juxtaposer un nombre quelconque de pyramides à faces équilatérales.

© Robert FERRÉOL 2007