Rhombicosidodécaèdre

RHOMBICOSIDODÉCAÈDRE
Rhombicosidodecahedron, Rhombenikosidodekaeder

.

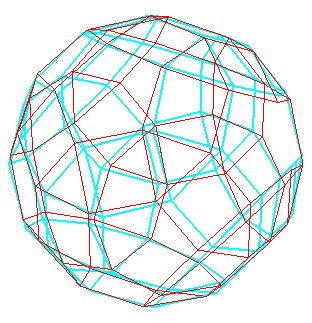
Anaglype à regarder avec des lunettes rouge (à gauche) et bleu (à droite).
Programme Maple de tracé.

Famille polyèdre semi-régulier ou polyèdre d'Archimède

Historique solide connu d'Archimède (III^e s. av. J.C.)

Autre nom petit rhombicosidodécaèdre

Dual hexacontaèdre trapézoïdal :

Faces 20 triangles, 30 carrés, 12 pentagones

Sommets 60 sommets de degré 4, de code de Schläfli 3.4.5.3

Arêtes 120 arêtes de longueur a ; angle dièdre entre un carré et un pentagone :
angle dièdre entre un carré et un triangle : .

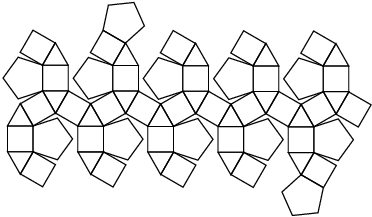
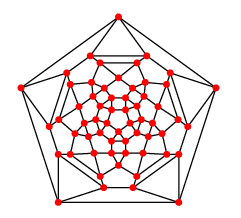
Patron et graphe

Diamètres sphère inscrite dans les pentagones : ; dans les carrés : ; dans les triangles :
intersphère (tangente aux arêtes) : ; sphère circonscrite : .

Mensurations volume : aire :
coefficient isopérimétrique : .

Construction

dodécaèdre, ou icosaèdre tronqué aux arêtes et aux sommets :

la troncature forte des sommets de l'icosidodécaèdre donne un polyèdre équivalent au rhombicosidodécaèdre, mais qui n'est pas semi-régulier (les carrés sont ici des rectangles)

Polyèdres dérivés 12 polyèdres de Johnson
le petit dodécicosidodécaèdre et le petit rhombidodécaèdre qui ont les mêmes arêtes
le petit dodécaèdre tronqué étoilé qui a les mêmes sommets
cf aussi le petit icosicosidodécaèdre, le petit dodécicosaèdre et le petit dodécicosidodécaèdre ditrigonal dont l'enveloppe convexe des sommets est équivalente au rhombicosidodécaèdre.
Idem pour le grand dirhombicosidodécaèdre.

Plans de symétrie 9

Axes de rotation

15 axes passant par les milieux de 2 arêtes opposées joignant des hexagones (1 rotation d'ordre 2 par axe)

10 axes passant par les centres de 2 triangles opposés (2 rotations d'ordre 3 par axe)

6 axes passant par les centres de 2 pentagones opposés (4 rotations d'ordre 5 par axe)

Groupe des isométries = celui de l'icosaèdre.

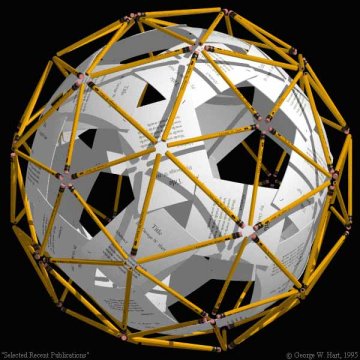
Magnifique sculpture virtuelle dûe à George Hart ; les rectangles de papier sont posés sur les arêtes d'un dodécaèdre, simulent donc un rhombicosidodécaèdre.
Les "allumettes" jaunes joignent les centres des faces du précédent, sauf ceux des triangles et ne représentent donc pas le dual. Les centres des pentagones forment un icosèdre, et l'on voit que chaque triangle de cet icosaèdre est partagé en 4 triangles : les allumettes forment donc une géode de type (2,0).

polyèdre suivant polyèdre précédent courbes 2D courbes 3D surfaces fractals polyèdres

.
Anaglype à regarder avec des lunettes rouge (à gauche) et bleu (à droite). Programme Maple de tracé.