Dodécaèdre adouci

DODÉCAÈDRE ADOUCI
Snub dodecahedron, abgeschrägtes Dodekaeder

Vues Povray de cette page réalisées par Alain Esculier.

Famille polyèdre semi-régulier ou polyèdre d'Archimède

Historique solide connu d'Archimède (IIIe s. av. J.C.)

Autre nom dodécaèdre camus

Dual 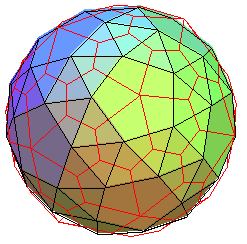hexacontaèdre pentagonal

Faces 80 triangles et 12 pentagones

Sommets 60 sommets de degré 5, de code de Schläfli 3⁴.5

Arêtes 150 arêtes de longueur a ; angle dièdre entre un pentagone et un triangle 152° 55' 48'' ; entre deux triangles : 164° 10' 31".

Patron et graphe

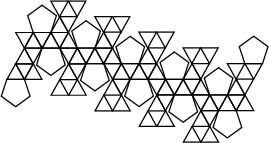Diamètres sphère inscrite dans les pentagones : 3,96.a ; dans les triangles : 4,15.a
intersphère (tangente aux arêtes) : 4,19.a; sphère circonscrite : 4,31.a.

Mensurations volume : 37,62.a³ aire : 55,29.a²
coefficient isopérimétrique : 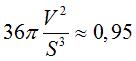(maximal pour les polyèdres semi-réguliers)

Coordonnées
des sommets voir wikipedia

Construction

adoucissement du dodécaèdre ou de l'icosaèdre

remarquons qu'on passe (combinatoirement) du rhombicosidodécaèdre (ci-contre) au dodécaèdre adouci en "partageant" les carrés (verts ci-contre) en deux triangles :

Plans de symétrie aucun ; le dodécaèdre adouci est donc "chiral" : voir les 2 versions ci-dessus.

Axes de rotation

6 axes passant par les centres de 2 pentagones opposés
(4 rotations d'ordre 5 par axe)

10 axes passant par les centres de 2 triangles opposés (2 rotations d'ordre 3 par axe)

15 axes passant par 2 arêtes opposés (1 rotation d'ordre 2 par axe)

Groupe des isométries = groupe des rotations du dodécaèdre ou de l'icosaèdre (pas d'isométrie négative).

Ce globe abat-jour semble avoir la structure du dodécaèdre adouci ; les 12 pentagones ont été séparés chacun en 5 cerfs-volants, et les 80 triangles regroupés en 40 losanges non plans, d'où 100 losanges ou cerfs-volants.

polyèdre suivant polyèdre précédent courbes 2D courbes 3D surfaces fractals polyèdres