;
by convention, we set 
.
Caracterisation : orientable connected compact surface without boundary of genus n.
The Euler characteristic of the n-torus is equal to 2–2n.
| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
n-HOLED TORUS
The notion of n-holed torus, or n-torus,
or n-uple torus, or sphere with n handles, refers to any
topological space homeomorphic to the connected
sum of the simple torus n times with itself: ;
by convention, we set .
Caracterisation : orientable connected compact surface
without boundary of genus n.
The Euler
characteristic of the n-torus is equal to 2–2n.
| The double torus is informally called "pretzel". On the right, a mathematical pretzel composed of two loops that are Viviani curves and an arc of a circle. |  |
 |
An algebraic
pretzel of degree 4, with 2 planes
of symmetry, and equation  ;
this equation was knocked up from that of the figure-eight:  ,
in order to thicken it. |
 |
Starting from the lemniscate
of Bernoulli, we get the figure below, with equation:
 . |
 |
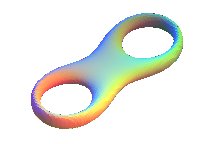A triple algebraic torus, based on the regular
trifolium, with equation:  . |
 |
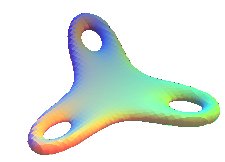A quadruple algebraic torus, with equation:  . |
 |
| The n-holed torus is also informally called "fougasse": opposite, a fougasse with 6 holes. |
 |
| The rulpidon
of Ulysse Lacoste is a solid having four orifices, the surface
of which is however homeomorphic to the torus with three holes (enlarge
one of the orifices; the other three form
the holes). 
Animation by Alain Esculier |
 |
Do not mistake the n-torus
with the n-dimensional torus,
;
in particular, 
.
| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017