Cubic surface

CUBIC SURFACE

The cubic surfaces are the algebraic surface of degree 3 (and not the surfaces shaped like a cube... If you are looking for such a surface, see here).

Examples:
    - the rational cubics
    - the Cayley surface
    - the Clebsch surface
    - the neiloid
    - the Goursat tetrahedral surfaces

surface x y z = a³: surface z³ = axy, projectively equivalent to the previous one:

A property that has really excited mathematicians is that any smooth complex surface of degree 3 contains exactly 27 straight lines (whereas any smooth surface of degree 2 is a ruled surface, and a smooth projective surface of degree greater than or equal to 4 may not contain any lines).

In real projective geometry, this Salmon-Cayley theorem becomes: any projective smooth surface of degree 3 contains exactly 3, 7, 15 or 27 real lines (result due to Schläfli); the Clebsch surface is the only one, up to homography, to have 27 real lines. The surface of Henrici also possesses 27 lines, but each is nonuple.

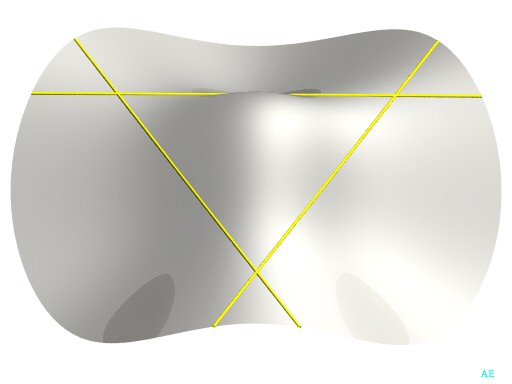
Example with 3 real lines:

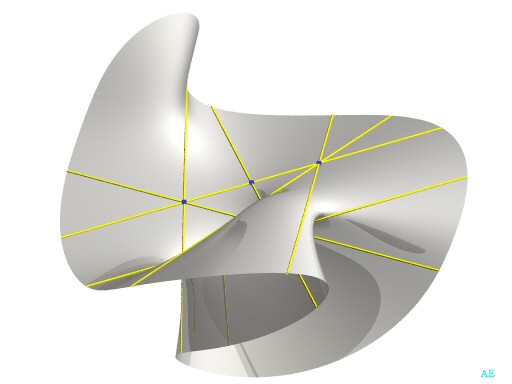
Contains the line and the two other lines obtained by permutation of the coordinates.

Example with 7 real lines:
Contains the 4 lines and the 3 lines at infinity of the planes xOy, yOz and xOz.
In the view opposite, the 3 lines at infinity were brought back at finite distance.

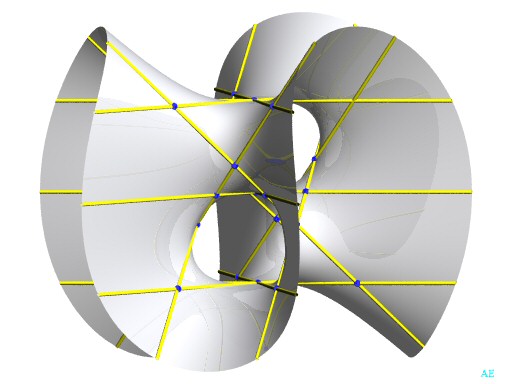
Example with 15 real lines:

Contains the 9 horizontal lines:,
the 2 lines,
and the 4 lines

The Danish mathematician C. Juel extended the notion of algebraic surface of degree 3 to that of surface of order 3, that intersects with any non included line at a maximum number of 3 intersection points; he then proved, be the surface algebraic or not, that any smooth surface of order 3 contains 3, 7, 15 or 27 lines.
This silver model of a surface of order 3, made by the jeweler Evald Nielsen of Copenhagen, was offered to Juel for his 70th birthday in 1925, during his scientific jubilee. After Juel's death, this piece was given by the family to the Copenhagen Institute of Mathematics where it is still displayed today.
Give me your opinion: how many lines are included in this surface? 3, 7, 15, or 27?
Picture provided by L. G. Vidiani.

WEBOGRAPHY
Oliver Labs's PhD thesis: enriques.mathematik.uni-mainz.de/labs/diplomArbeit_OliverLabs.pdf
Website dedicated to cubic surfaces, by Oliver Labs: algebraicsurface.net
Knörrer and Miller : Topologische Typen reeller kubischer Flächen, Mathematische Zeitschrift volume 195; pp. 51 - 91
A. henderson, the 27 lines upon the cubic surface, Hafner, N. Y., 1911
B. Segre, the non-singular cubic surfaces, Oxford, 1942.

next surface previous surface 2D curves 3D curves surfaces fractals polyhedra