
| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
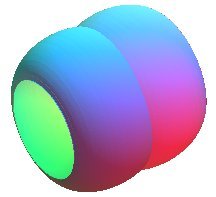
DELAUNAY SURFACE
 |
 |
| Surface studied by Delaunay in 1841, Lindelöf in 1863, Plateau in 1873. |
| Cartesian parametrization: |
The Delaunay surfaces are the surfaces of revolution generated by the rotation of the Delaunay roulettes around their base.
The surfaces associated to an elliptic roulette are called
onduloids
and those associated to a hyperbolic roulette nodoids.
Since the parabolic roulette is the catenary, the associated
surface is none other than the catenoid
(case of the zero mean curvature).
The Delaunay surfaces have the remarkable property of being the only surfaces of revolution with constant mean curvature (if we include the sphere, which is a limit case), the case of zero curvature being obtained for the catenoid.
As a consequence, a layer of soap with an axis of revolution assumes the shape of a Delaunay surface.
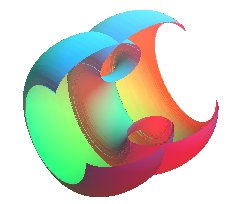
See also: Histoires
de bulles et de doubles bulles, La Recherche, N°303 - 11/1997
and www.gang.umass.edu/gallery/cmc/
| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL , Jacques MANDONNET 2017