Cartesian parametrization: . Simply periodic minimal surface.

Catalan's minimal surface is the surface obtained by taking  (and then ) in the Weierstrass parametrization of a minimal surface: .
 
 

With   in the parametrization above, we get ; the projection of the coordinate lines at constant r on a horizontal plane are trochoids, and the coordinate lines at constant v are parabolas.  Moreover, the section of Catalan's surface by xOy is a cycloid, which is a geodesic of the surface.
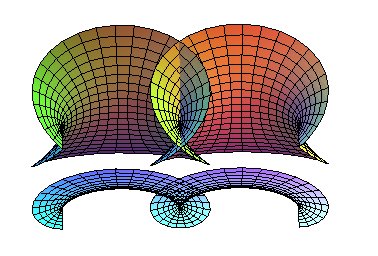Opposite, an animated view of the surface "associated" to Catalan's surface, i.e. the surfaces obtained by taking  in the Weierstrass parametrization. Their parametrization is .

Here is the original text by Catalan in which he publishes his surface as an example of application of a general formula for minimal surfaces:

The surface represented by these three equations can be generated in the following way:
Define OSA the cycloid described by the point S belonging to the circumference CI, and the cycloidOPB, envelope of the moving radius CS, P being the contact point. If we create, in a plane perpendicular to that of the figure, a parabola the projection of the directrix of which is P, and such that S is the vertex, this curve (with variable size) generates the surface.

Do not mistaken this surface for the Catalan surfaces.

next surface

previous surface

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL  2017