Ludwig Schläfli (1814-1895) : mathématicien suisse. Autre nom : double sixain.

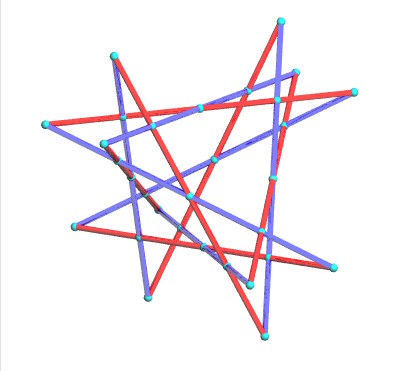
Un double-six est un ensemble de 12 droites de l'espace projectif de dimension 3, dont la notation habituelle, due à Schläfli, est matricielle :

Le nombre six est la valeur maximale de n telle qu'un ensemble de 2n droites ait cette propriété (démonstration de ce fait).

Pour construire un double-six, on peut partir d'une droite  ayant 5 sécantes  telles qu'aucune d'entre-elles ne soit incluse dans la quadrique engendrée par 3 des 4 autres droites.
Quatre droites parmi les 5 sécantes  ont  pour sécante commune et aussi une autre sécante commune : si {i, j, k, l, m}={1, 2, 3, 4, 5}, notons  la sécante commune autre que  à  ; on montre que  ne rencontre pas  : pour terminer le double-six il ne manque plus que la droite  : sécante commune à  ne rencontrant pas  : le théorème (difficile) du double-six affirme que cette droite existe.

Chaque droite du double-six en rencontre exactement 5 autres ; il y a donc  points d'intersection dans le double-six.
 

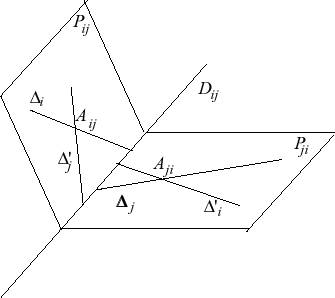Les 30 couples de droites sécantes  engendrent 30 plans , et les 15 paires de plans  sont formées de plans se coupant suivant 15 droites .

 
 

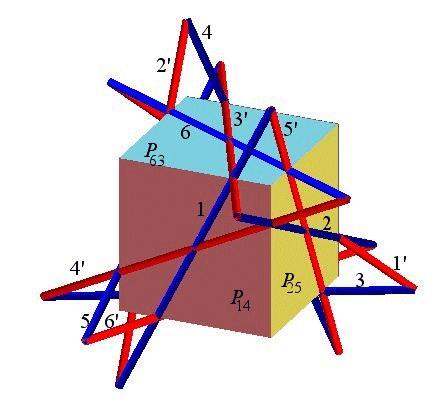Figure du double six avec les six droites  en bleu (notées i tout seul pour simplifier), et les six droites  (notées i') en rouge ;  chaque droite rouge rencontre exactement 5 droites bleues et vice versa. Cette vue affine a été choisie de sorte que les 6 plans  , ,    soient les 6 faces d'un cube. De la sorte, les 3 droites  sont les 3 droites de l'infini des faces du cube.

 
 

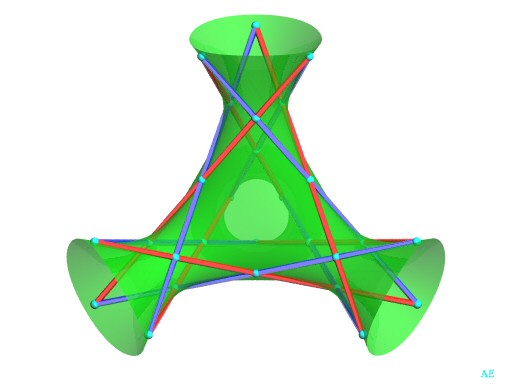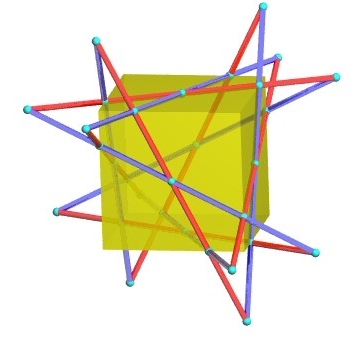
	Il existe une unique surface cubique lisse (S) contenant les 12 droites du double-six. Pour le double-six représenté ci-dessus, où le cube choisi a pour sommets  etc, et la droite  passe par , la surface cubique a pour équation : .
	Les 27 droites de cette surface sont les 12 droites du double-six (en rouge et bleu ci-contre) plus les 15 droites (en jaune) définies ci-dessus. (mais rappelons que dans la représentation ci-contre, les 3 droites  sont les 3 droites de l'infini des faces du cube et que donc il n'y a que 12 droites jaunes visibles)

La figure que forment les 27 droites s'appelle l'eikosiheptagramme (eikosihepta = 27 en grec).
Dans cette configuration, chaque droite en rencontre exactement dix autres :
    - chaque droite jaune est sécante avec les 4 droites  rouges et bleues et avec les  droites  jaunes pour (démonstration de ce fait).
    - chaque droite rouge est sécante avec les 5 droites  bleues  et les 5 droites  jaunes.
Il existe donc  paires de droites non sécantes.

On montre alors qu'il existe dans l'eikosiheptagramme exactement 36 doubles-six :
    - le double-six de départ N.
    - les  doubles-six du type  dits "syzygétiques" à N
    - les  doubles-six du type , dits "azygétiques" à N.

Le groupe des permutations des 27 droites respectant les incidences des droites possède donc 6 ! . 2 . 36 = 51 840  éléments ; il est isomorphe au groupe de Weyl W(E₆) et son sous-groupe des permutations paires est isomorphe au groupe projectif symplectique PSp₄(F₃) qui n'est pas simple.

Chacun des 30 plans  contient 3 droites de la surface (S) ( et): il est appelé plan tritangent (puisque tangent à la surface en 3 points).

Mais il existe, issus des doubles-six ci-dessus,  autres plans tritangents engendrés par les 15 trios de droites sécantes deux à deux :  ; on montre que ces 45 plans tritangents sont les seuls : chaque droite est commune à 5 plans tritangents.

Les incidences des divers éléments de l'eikosiheptagramme sont résumés dans le tableau ci-dessous :
 

....rencontre	points	droites	plans tritangents	double-six	eikosiheptagramme
chaque point...	1	2	1	8	1
chaque droite...	10	10	5	16	1
chaque plan tritangent...	3	3	15	36	1
chaque double-six...	30	12	45	36	1
l'eikosiheptagramme...	135	27	45	36	1

 

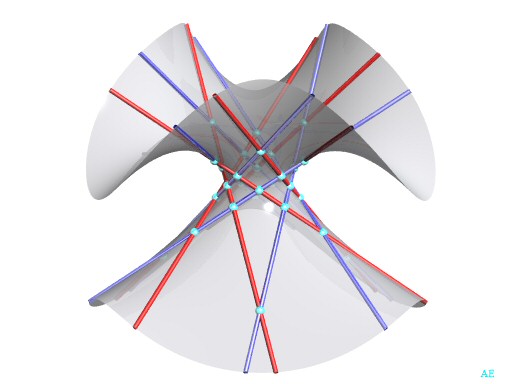Voici une vue du double-six principal de la surface de Clebsch.

 

Ceci n'est un double-six qu'en apparence : chaque droite bleue rencontre 5 droites rouges, mais aussi la sixième, à l'infini ! Dans un vrai double-six, il ne peut y avoir plus de 3 droites de chaque famille sur une même quadrique (voir cette figure)

 

WEBOGRAPHIE Applet java pour le double-six, sur le même site : enriques.mathematik.uni-mainz.de/cubicsurface/background/background_frame.php3?shortname=doublesix Modele en tiges du double-six : www.math.arizona.edu/~models/Wire_models/source/2.html

© Robert FERRÉOL , Alain ESCULIER 2003