Surface de Clebsch

SURFACE (DIAGONALE CUBIQUE) DE CLEBSCH
Clebsch surface, clebsche Diagonalfläche

Surface étudiée par Clebsch en 1871 A. Clebsch, Ueber die Anwendung der quadratischen Substitution auf die Gleichungen 5ten Grades und die geometrische Theorie des ebenen Fünfseits, Math. Ann. IV (1871), 284–345.
Alfred Clebsch (1833-1872) : mathématicien allemand.
Lien : catalogue des modèles du laboratoire de mathématiques de Besançon.

Équation pentaédrique dans : .
Surface cubique lisse à points hyperboliques.

La surface de Clebsch est la surface donnée par l'équation ci-dessus.
C'est, à homographie près, la seule surface cubique dont le groupe des homographies la laissant invariante est le groupe S₅ des permutations de cinq objets (cf. l' invariance par les 120 permutations des coordonnées ).

Elle possède la particularité que les 27 droites que comporte toute surface cubique lisse sont toutes réelles.
Ces 27 droites se répartissent en deux groupes :

1) les 15 droites dites diagonales ou hyperboliques avec ; ces droites sont ainsi appelées car ce sont les diagonales du pentaèdre dont les faces sont les 5 plans tritangents de Sylvester : et les sommets (points communs à 3 faces) les 10 points dits d'Eckardt ; la droite , joignant les deux points d'Eckardt et , est en effet l'une des 3 diagonales du quadrilatère complet découpé sur la face F_m par les 4 autres faces.
Les trois diagonales , et issues de sont coplanaires (elles joignent aux points alignés sur l'arête ) ; leur plan est l'un des 10 plans tritangents d'Eckardt.
Chaque point d'Eckardt est commun à 4 plans d'Eckardt .
Face Fm du pentaedre de Sylvester avec les 6 points d'Eckardt et les trois diagonales incluses dans la cubique.

Vue générale du pentaèdre.

La surface de Clebsch est, à homographie près, la seule surface cubique à comporter 10 points triples d'Eckardt.

2) Les 12 droites du double-six principal
avec , {k, l} = {1,2,3,4} \ {i, j}, où est le nombre d'or, solution positive de .
Dans l'espace complexe, ces droites ont une définition très simple : ce sont les droites joignant le point de coordonnées homogènes à son conjugué , où est l'ensemble des 5 racines cinquièmes de 1 (en normalisant u₁ à 1, on retrouve bien les 12 possibilités) ; par exemple, la droite correspond à où .

On montre que ces douze droites forment le "double-six"

dit principal (il en existe 35 autres). Deux droites sont dans la même ligne du double-six si la permutation faisant passer des indices de l'une à ceux de l'autre est paire.

Voici diverses représentations affines de cette surface :

Le changement de coordonnées donne l'
Équation homogène : , d'où l'équation affine :
.
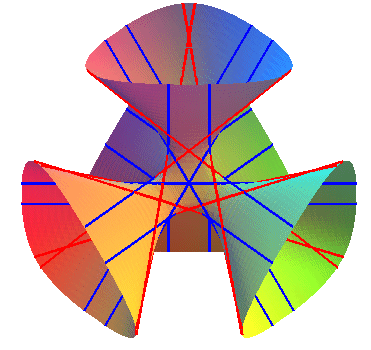
Cette représentation présente l'inconvénient que le plan et ses 3 droites incluses sont rejetés à l'infini.
ici, les diagonales en bleu, et le double-six en rouge.

Représentation affine choisie par Clebsch et Klein en 1872 pour le modèle créé par le sculpteur Adolf Weiler :

Le changement de coordonnées défini par, soit
donne pour k = 4, l= 3 (choisis pour des considérations esthétiques) l'
Équation homogène :
Équation cartésienne affine associée :
Soit : .
Cette transformation a été choisie de sorte que la surface enclidienne obtenue soit à symétrie de rotation d'ordre 3 autour de Oz ; les 4 premiers plans de Sylvester forment un tétraèdre isocèle de base F₄, et F₅ est parallèle à F₄, de sorte que les points de Eckardt S₁₂, S₂₃, et S₃₁ sont à l'infini.

Voici des représentations utilisant cette équation : remarquer les droites parallèles se coupant en un point d'Eckardt à l'infini.

En jaune les 15 diagonales avec les points d'Eckardt, en rouge et bleu le double six principal ; remarquer le tétraèdre formé des 4 premiers plans de Sylvester.

Sculpture à la cafétéria de l'université Heinrich Heine de Düsseldorf.

Voici une transformation rationnelle telle que les 4 premiers plans de Sylvester forment un tétraèdre régulier :

Le changement de coordonnées défini par , soit donne l'
Équation homogène :

Équation cartésienne affine associée :

Soit : .
Les 4 premiers plans de Sylvester forment le tétraèdre régulier de sommets les points d'Eckardt :, les 3 autres points d'Eckardt à distance finie étant les milieux des arêtes issues de A_45
:. Les points sont à l'infini.
ici, les diagonales en bleu, et le double-six en rouge.

Voici une série de vues d'une représentation où les 10 points d'Eckardt sont à distance finie :

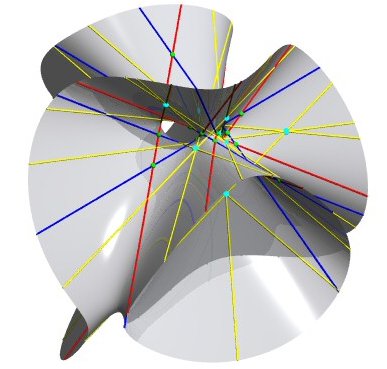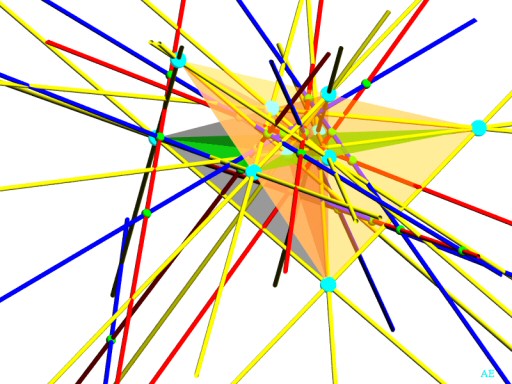Voir aussi la surface de Cayley.

Le modèle ci-dessus provient du Palais de la Découverte, mais n'est pas exposé actuellement.
Gravure de Patrice Jeener, avec son aimable autorisation.

WEBOGRAPHIE
Page d'Alain Esculier sur le sujet : aesculier.fr/fichiersMaple/ClebschDroites/ClebschDroites.html
Une version d'équation simple : x^3+y^3+z^3=4xyz+x+y+z, trouvée par Alain Esculier
Autre site, par le même : enriques.mathematik.uni-mainz.de/csh/playing/galery/famous.html
B. Hunt, The Geometry of Some special Arithmetic Quotients, Lecture Notes in Mathematics, vol.1637, Springer-Verlag 1996.
Un texte en allemand simple et clair : mathedidaktik.uni-koeln.de/fileadmin/MathematikFiles/kaenders/kaenders_06.pdf

surface suivante surface précédente courbes 2D courbes 3D surfaces fractals polyèdres