Les surfaces cubiques sont les surfaces algébriques de degré 3 (et non les surfaces ayant la forme d'un cube... Si vous cherchez une telle surface, voir ici).

Exemples :
    - les cubiques rationnelles
    - la surface de Cayley
    - la surface de Clebsch
    - le neiloïde
    - les surfaces tétraédriques de Goursat
    - La surface d'Henrici
 

Surface x y z = a3  :

Surface z3 = axy, projectivement équivalente à la précédente :

Une propriété qui a beaucoup excité les mathématiciens est que toute surface lisse projective complexe du troisième degré contient exactement 27 droites (alors que toute surface lisse projective complexe du deuxième degré est réglée, et qu'une surface lisse projective complexe de degré supérieur ou égal à 4 peut ne pas contenir de droite).

En géométrie projective réelle, ce théorème de Salmon-Cayley devient : toute surface lisse projective réelle du troisième degré contient exactement 3, 7, 15, ou 27 droites réelles (résultat dû à Schläfli) ; la surface de Clebsch est la seule, à homographie près, à posséder les 27 droites réelles, et distinctes. La surface d'Henrici possède aussi 27 droites, mais chacune est nonuple.
 

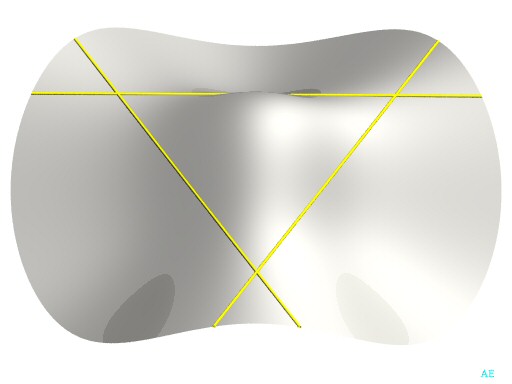
Exemple avec 3 droites réelles : Contient la droite  et les deux autres obtenues par permutation des coordonnées.
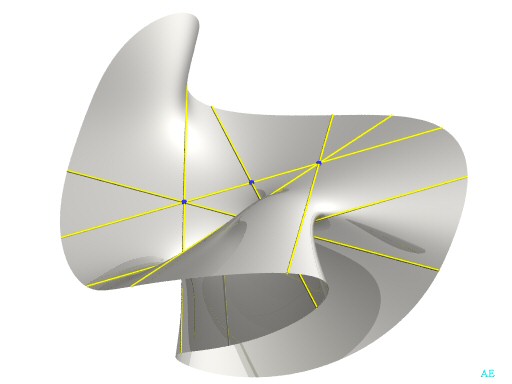
Exemple avec 7 droites réelles : Contient les 4 droites  et les 3 droites de l'infini des plans xOy, yOz et xOz. Dans la vue ci-contre, les 3 droites à l'infini ont été ramenées à distance finie.
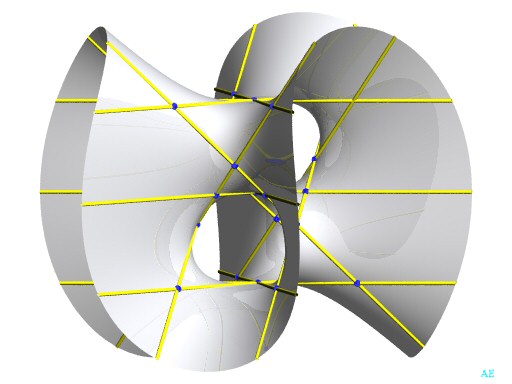
Exemple avec 15 droites réelles : Contient les 9 droites horizontales :, les 2 droites,  et les 4 droites

 

Le mathématicien danois C. Juel a étendu la notion de surface algébrique du troisième degré à celle de surface du troisième ordre, qui rencontre toute droite non incluse en un maximum de 3 points ; il a alors démontré, indépendamment de l'algébricité, que toute surface lisse du troisième ordre possède 3, 7, 15 ou 27 droites. Ce modèle en argent d'une surface du troisième ordre, réalisé par le joaillier Evald Nielsen de Copenhague, a été offert à Juel pour son 70ème anniversaire en 1925, lors de son jubilé scientifique. Après la mort de Juel, cette pièce a été donnée par la famille à l'Institut Mathématique de Copenhague où elle se trouve encore actuellement. Donnez-moi votre avis : combien de droites sont incluses dans cette surface ? 3, 7, 15, ou 27 ?  Photo fournie par L. G. Vidiani.

 

WEBOGRAPHIE Mémoire de master de François LE : Sur les vingt-sept droites des surfaces cubiques : approche historique Thèse d'Oliver Labs : enriques.mathematik.uni-mainz.de/labs/diplomArbeit_OliverLabs.pdf Site dédié aux surfaces cubiques, par Oliver Labs : algebraicsurface.net Knörrer and Miller : Topologische Typen reeller kubischer Flächen, Mathematische Zeitschrift volume 195; pp. 51 - 91 A. Henderson, the 27 lines upon the cubic surface, Hafner, N. Y., 1911 B. Segre, the non-singular cubic surfaces, Oxford, 1942.

 

surface suivante

surface précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL , Alain ESCULIER 2011