DINOSTRATUS QUADRATRIX

| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
DINOSTRATUS QUADRATRIX

| Curve studied by Hippias of Elis in 430 BC and by Dinostratus in 350 BC.
Dinostratus (4th century BC): Greek mathematician. Other name: Hippias sectrix. |
|
Cartesian-polar parametrization: Polar equation: 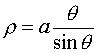 , where , where |
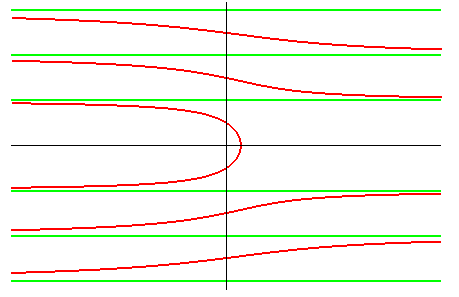 |
| The Dinostratus quadratrix is the locus of the intersection points between a line in a uniform translation and a line in a uniform rotation, the two lines coinciding at some moment. In that capacity, it is a limit case of Maclaurin sectrix, when one of the poles is at infinity. |
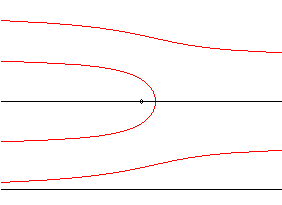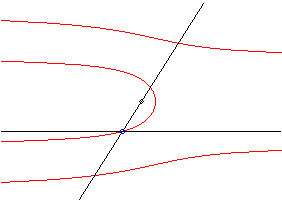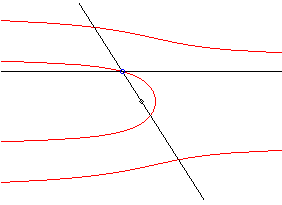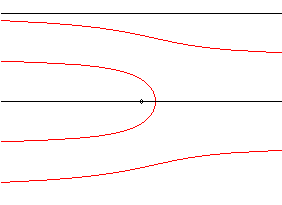 |
| It is the inverse with respect to O of a cochleoid. | 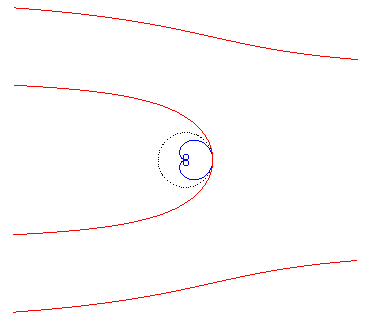 |
| Consider the complex parametrization: |
 |
The Dinostratus quadratrix also is the projection on a plane perpendicular to the axis of the section of a right helicoid by a plane containing a generatrix of the helicoid.
As you can tell by the name, this curve is a quadratrix; indeed:.
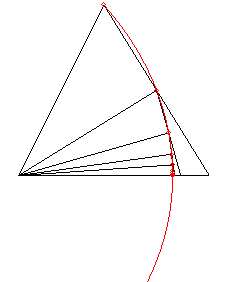
But it was first considered by Hippias as a trisectrix and even an n-sectrix; indeed .
If we study the general case of the loci of intersection points between a line in uniform translation and a line in uniform rotation, we get the following curves, that also are multisectrices:
|
Cartesian-polar parametrization: Polar equation: 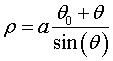 , where , where Cartesian equation: |
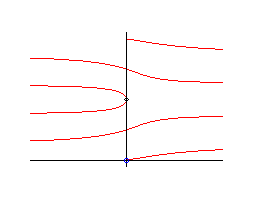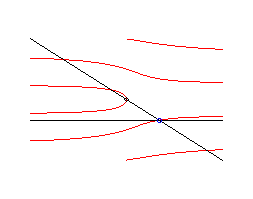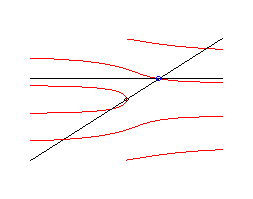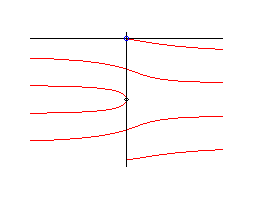
Case where q0 = p/2 , with equation |
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017