Curves studied by Euler in 1750 and 1783, Cesaro in 1887.

The pseudocycloidal curves are the curves satisfying an intrinsic equation of the type , by analogy with the cycloidal curves, which satisfy: . In other words, they are the curves for which, when they roll without slipping on a line, the centre of curvature describes a hyperbola an axis of which is parallel to the line (see Mannheim curve).

There are two cases, depending on the sign of the above constant cte.

First case, cte <0: PARACYCLOID
 
 

Cartesian parametrization: . Cartesian tangential angle: . Curvilinear abscissa: . Radius of curvature: . Intrinsic equation 1: .

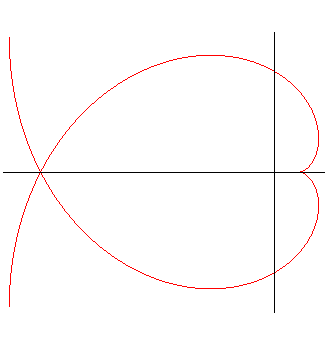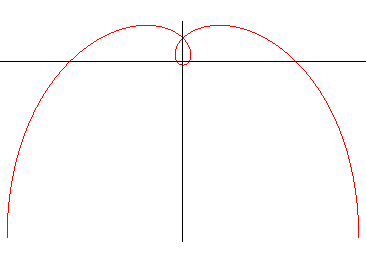
Second case, cte >0: HYPERCYCLOID (be careful, the word hypercycloid is also used instead of epicycloid)
 
 

Cartesian parametrization: . Cartesian tangential angle: . Curvilinear abscissa: . Radius of curvature: . Intrinsic equation 1: .

REMARK: the paracycloid is the negative pedal of the spiral of the hyperbolic sine , and the hypercycloid is the negative pedal of the spiral of the hyperbolic cosine . Furthermore, they are the evolutes of one another.
 
 

next curve

previous curve

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL  2017