Other name: anticaustic, but this word has another meaning on this website. Ref: (Zwikker p. 144)

 

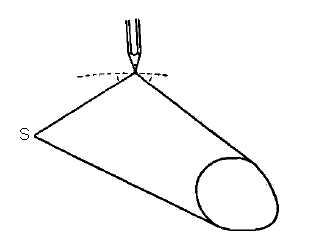
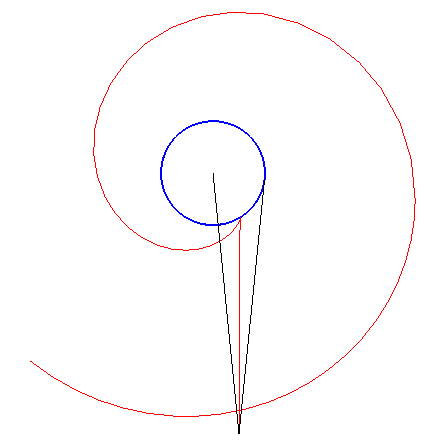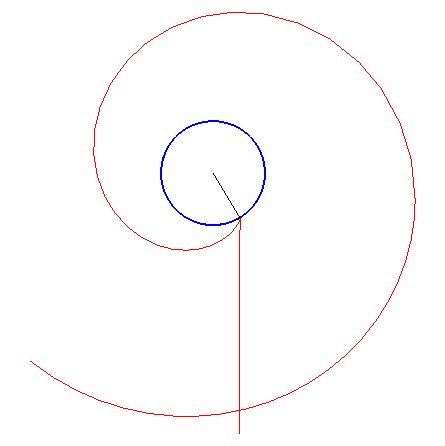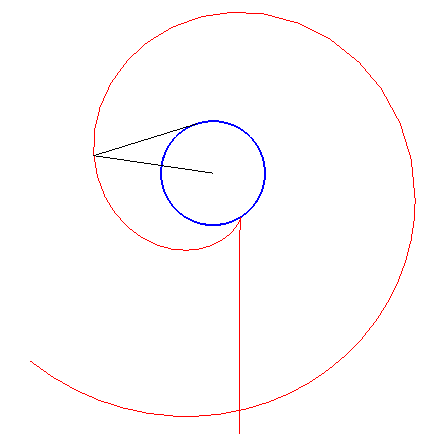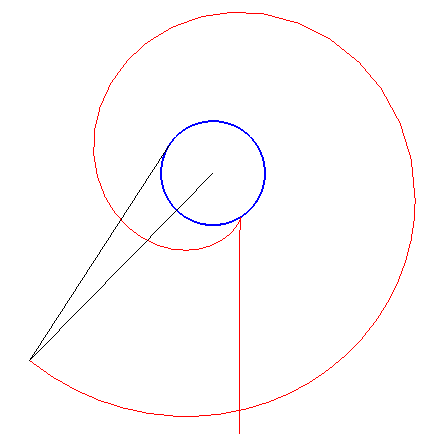
The notion of inverse caustic (by reflection) with respect to a point S of a curve  refers to any curve  for which the caustic by reflection with respect to S is . If  is the current point on  and M is the one on , the condition is that the normal at M to the inverse caustic always be a bisector of . Since the direct caustic is the evolute of the orthotomic, the inverse caustics are the curves for which the orthotomic is one of the involutes of the initial curve. The diagram opposite shows the construction of M when the point N on the involute is given.

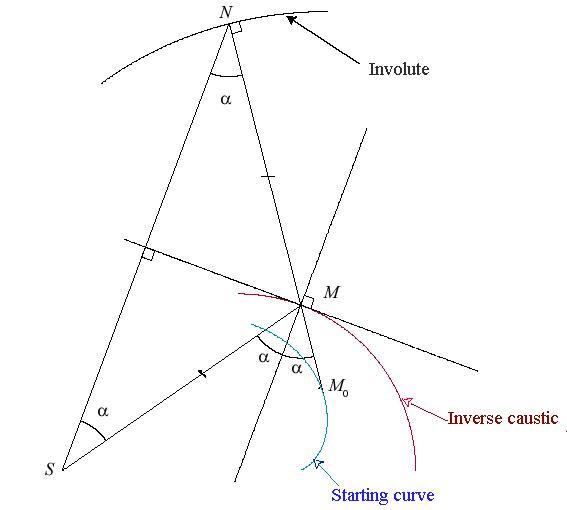
When the initial curve is convex, we therefore, mechanically, get a portion of inverse caustic by wrapping an inextensible cord around the curve and making it pass by S and a pencil that will then trace the inverse caustic (generalisation of the gardener's method for tracing ellipses). Various lengths of the cord will result in various inverse caustics.

 

Case of the inverse caustic of a circle with respect to its centre:
 
 

Cartesian parametrization: , For a caustic equal to the circle with centre O and radius 2a.

 
 
 

The light rays emitted by the centre of the circle and reflected by the red curve envelope the blue circle. We get the inverse caustic by unwinding, under tension, a wool ball one the extremities of which is attached to the centre of the ball.

next curve

previous curve

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL  2017