Epicycloid

EPICYCLOID

Curve studied by Hipparchus in the 2nd century BC, Dürer in 1525, RØmer in 1674 and Daniel Bernoulli in 1725.
Prefix coming from the Greek epi "over".

The epicycloids are the curves described by a point on a circle (C) rolling without slipping on a base circle (C₀), the open disks with boundaries (C) and (C₀) being disjoint. Therefore, they are special cases of epitrochoids.

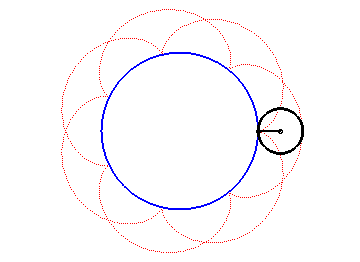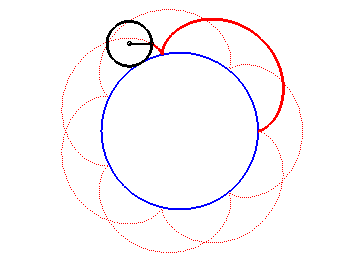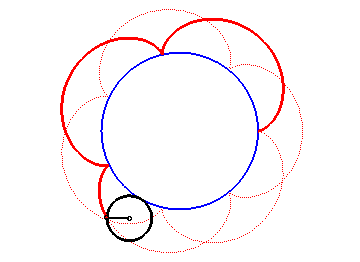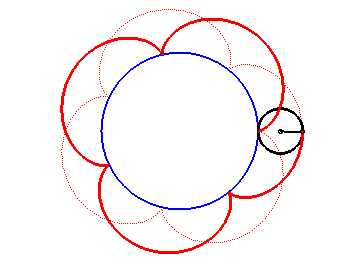
Complex parametrization:

where a is the radius of the base circle and

that of the rolling circle.
Cartesian parametrization:

.
Vector radius:

; polar angle given by

.
Curvilinear abscissa given by

(hence the differential equation

)
Two possible expressions for the curvilinear abscissa:
1)

.
Cartesian tangential angle:

.
Radius of curvature:

.
Intrinsic equation 1:

.
(

is the equation of an epicycloid if and only if d > c, with

)

Intrinsic equation 2: .
( is the equation of an epicycloid if and only if |B| < 1).
Pedal equation: .
Equation of the tangent at M(t): .
Length of an arch: .
Area of the surface located between the arch and its two tangents at the ends: .
For integer values of q, the total length is thus equal to times the length of the base circle, and the total area is equal to times the area of this circle.

The epicycloids are the curves composed of isometric arcs (the arches) joining at cuspidal points (obtained for ) in a finite number equal to the numerator of q if q is rational, or in an infinite number otherwise.
When q is rational, , the curve is algebraic and rational (take as a parameter).
Its looks like a regular polygon, crossed if m³ 2, with n vertices joined m points by m points by the curves located outside the circle (C₀).

The notation of simple epicycloid with n cusps (E_n) refers to the case q = n, i.e. when there are no crossovers.

q = 1: cardioid

q = 2: nephroid
q = 3
q = 4
q = 5

q = 1/2: double cardioid
q = 3/2
q = 5/2
q = 7/2
q = 9/2

q = 1/3
q = 2/3
q = 4/3
q = 5/3
q = 7/3

q = 1/4
q = 3/4
q = 5/4
q = 7/4
q = 9/4

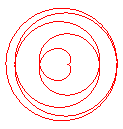
q = 1/5
q = 2/5
q = 3/5
q = 4/5
q = 6/5

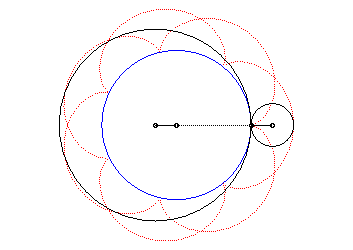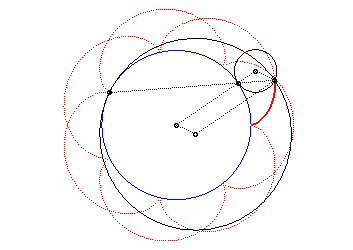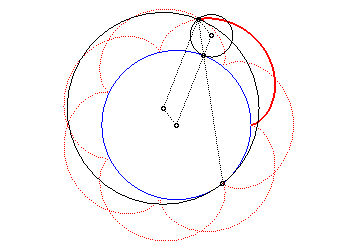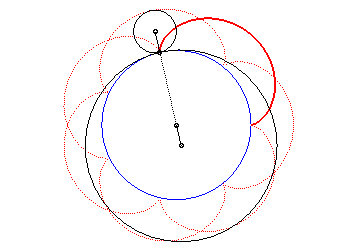The epicycloid is also the curve described by a point on a circle with radius () rolling without slipping on (C₀) while containing it (this constitutes the double generation of the epicycloid: see at pericycloid).

The epicycloid is the envelope of a diameter of a circle with radius twice that of (C), rolling without slipping on (C₀) externally.

It is also the envelope of a chord (PQ) of the circle with radius a + 2b (circle of the vertices of the epicycloid), while P and Q describe this circle in the same direction with the speed ratio constant and equal to q + 1 (this constitutes the Cremona generation).
Therefore, if we consider that planets have uniform circular movements on a plane around the Sun, the line that joins two planets envelopes an epicycloid (see, for example, this video).
It is finally the negative pedal with respect to O of the rose: .

Its evolute is its image by the direct similarity with centre O, ratio , and angle .

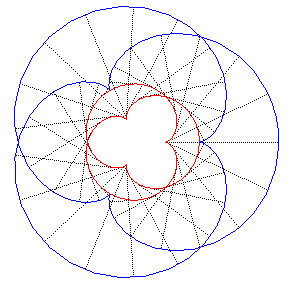One of its involutes is therefore a similar epicycloid; when the numerator of q is odd, the other involutes are auto-parallel curves.

Epicycloids can also be defined as the trajectories of a movement that is the sum of two uniform circular motions with same speed and in the same direction (with complex parametrization: with ).

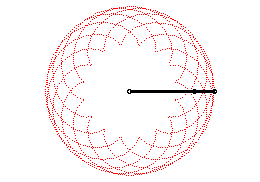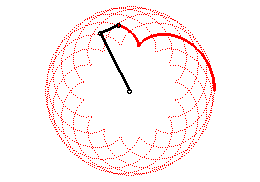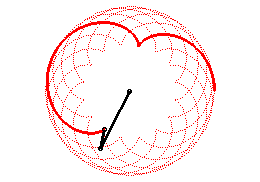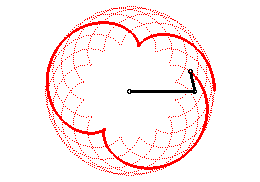The epicycloid is also the symmetric curve of the hypocycloid traced with the same circle.
For example, opposite, the epicycloid with 4 cusps is the symmetric curve of the astroid.

Epicycloids are also a special case of cycloidal curve, along with hypocycloids and the cycloid.

They also are the projections of spherical helices.

The differential equation shows, thanks to the Euler-Lagrange equation, that, as the cycloid, the epicycloid is a brachistochrone curve: it is the planar curve that minimises the travel time of a massive point moving freely along this curve, while the curve turns at constant speed around a fixed centre O, in the case where the speed of massive point cancels out when it is at distance a from O (when a = 0, the brachistochrone is then the logarithmic spiral).

We also find the epicycloids as the principal components of the Mandelbrot sets associated to .

See also in 3D the spherical epicycloids.

next curve previous curve 2D curves 3D curves surfaces fractals polyhedra

q = 1: cardioid	q = 2: nephroid	q = 3	q = 4	q = 5
q = 1/2: double cardioid	q = 3/2	q = 5/2	q = 7/2	q = 9/2
q = 1/3	q = 2/3	q = 4/3	q = 5/3	q = 7/3
q = 1/4	q = 3/4	q = 5/4	q = 7/4	q = 9/4
q = 1/5	q = 2/5	q = 3/5	q = 4/5	q = 6/5

Epicycloids can also be defined as the trajectories of a movement that is the sum of two uniform circular motions with same speed and in the same direction (with complex parametrization: with ).
The epicycloid is also the symmetric curve of the hypocycloid traced with the same circle. For example, opposite, the epicycloid with 4 cusps is the symmetric curve of the astroid.