Differential equations of the shadowing curves:
Hence, in polar coordinates:
Obvious solution:
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
SHADOWING CURVE
| Problem posed by Buray (a.k.a. Aubry) in 1896 (intermédiaire
des mathématiciens p. 35 and 93); curve studied
by Turrière in 1915.
Other names: pursuit curve in a row, pathfinder's curve, lion's curve. |
The shadowing curve is the trajectory of a moving
point M (the pursuer) that is, at all instants, aligned with a fixed
point O (the tree) and another moving point M0
(the pursuee). This corresponds to a true tail only when O is between
M
and M0, i.e. when the tree hides
M from M0 .
The problem has a determined solution if a condition
on the speed of M is imposed. We will consider here the case where
the speeds V and V0 of M
and M0 are proportional (V= kV0):
the shadowing curve obtained is independent from the speed profile of the
pursuee.
The notion is involutory, in the sense that the pursuee's
curve is a shadowing curve associated to the initial shadowing curve, if
k
is changed into 1/k.
| Conditions governing the movement of the pursuer,
in Cartesian coordinates: Differential equations of the shadowing curves: Hence, in polar coordinates: Obvious solution: |
The differential equation above proves that the solutions for any k are homothetic with ratio k to the solutions for k = 1, which is the only case we will study in the following.
Some special cases:
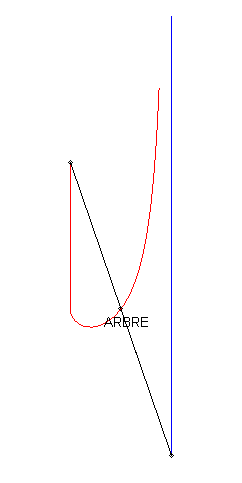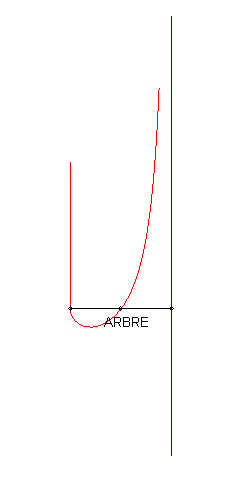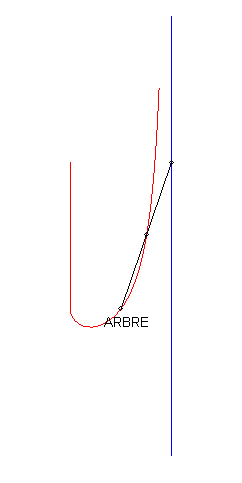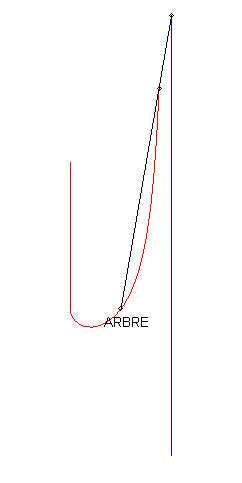
1) The pursuee's curve is linear.
| If we take with the initial condition: The polar differential equation of the curve can be written Relation between the pedal radius p and the abscissa: With Cartesian parametrization in the non-homothetic case: |
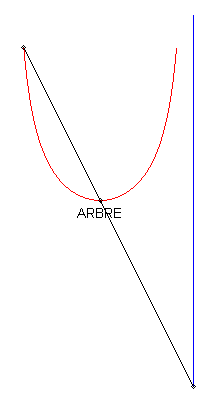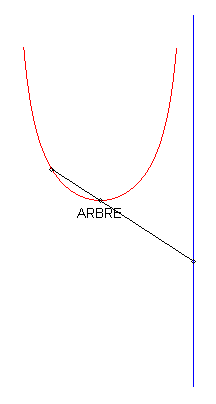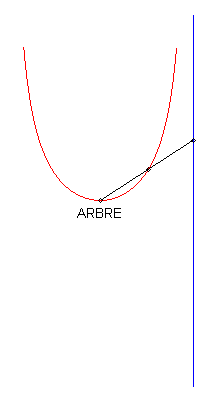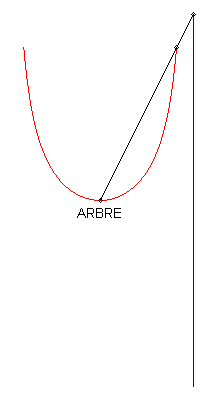
In the case where the tangent at O is horizontal, the curve looks like a Kappa, but the equation above shows that it is not one. |
 |
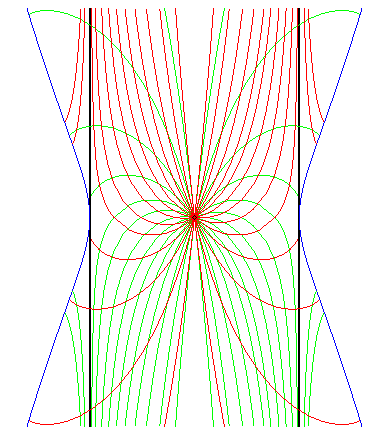 |
.gif) |
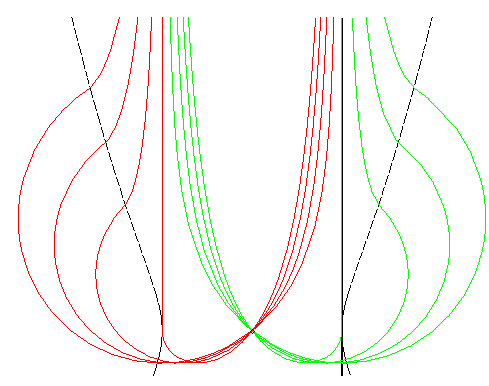
This representation of the real part of the solutions show that the pursuer goes only temporarily into the imaginary domain! |
2) The curve of the pursuee is a circle with centre O.
| The shadowing curve is then none other than a circle
passing
by O, or a circle with centre O in the homothetic case.
It can be noticed below that the pursuer and the pursuee can be swapped. Also note that the property exposed is just an application of the theorem of the central angle. This problem was also presented in the following way:
a man runs along an arena at constant speed; a lion, initially at the centre,
chases the man, with the same speed, in such a way that they are both aligned
with the centre; what is its trajectory, and how long does it take it to
catch up with the man?
|
 |
| In the previous case, the pursuer catches up with the pursuee, whereas it was not the case for the line; but even in the case of a bounded curve, it is possible for the pursuer never to catch up with the pursuee (and so, with the presentation above, for the lion never to get to the man); for example, with this spiral having an asymptotic circle: |

Despite indications of the contrary, here, the lion (red) never catches up with the man (blue), even though their mutual distance goes to 0. |
When the point O is at infinity, the shadowing curve becomes the curve of parallel pursuit.
See also the crab curve.
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017