,
soit 
car 
.
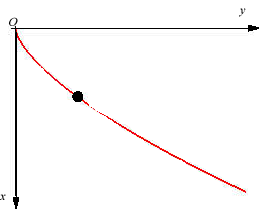
D'où les équations horaires du mouvement :
qui s'intègrent en : 
,
d'où l'équation de la trajectoire : 
.| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
COURBE ISOCHRONE DE LEIBNIZ
Isochronous
curve of Leibniz, leibnizsche isochrone Kurve
| Courbe étudiée par Leibniz en 1687 et par
Jacques Bernoulli en 1690.
Wilhelm Gottfried Leibniz (1646 - 1716) : philosophe et savant allemand. |
|
|
En prenant Ox comme verticale descendante et un
départ en O avec une vitesse horizontale nulle, la conservation
de l'énergie donne ,
soit
car .
D'où les équations horaires du mouvement :
qui s'intègrent en : ,
d'où l'équation de la trajectoire : . |
Une courbe isochrone de Leibniz est une courbe telle que si une particule descend par gravité le long d'elle, la composante verticale de la vitesse est constante, le champ de pesanteur étant supposé uniforme.
La solution est une parabole
semi-cubique, comme le montre la résolution ci-dessus. Remarquons
que la vitesse initiale au sommet de la parabole doit être égale
à égale à 
,
pour que la parabole semi-cubique 
soit isochrone ; la composante verticale de la vitesse est alors constante
égale à
(et la composante horizontale est proportionnelle à la racine carrée
du temps).
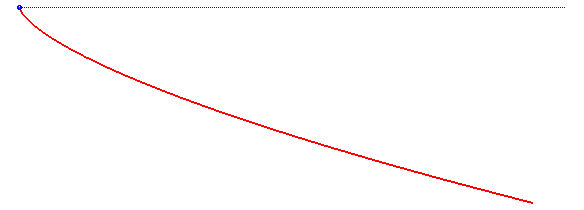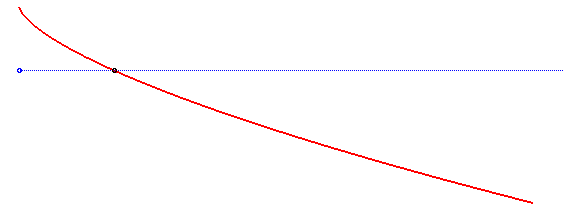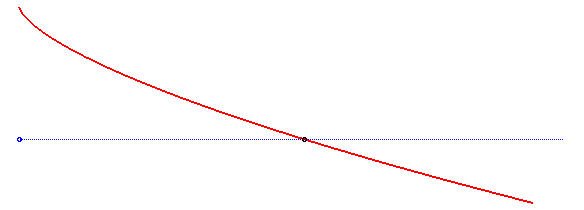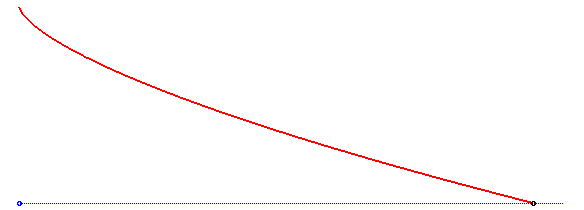
Dans cette résolution, le vecteur d'accélération de la pesanteur a été supposé constant ; si on le suppose seulement de norme constante, mais dirigé vers un point fixe à distance finie, on obtient les courbes appelées isochrones de Varignon.
Pour d'autres courbes de mouvement d'un point matériel
dans un champ de pesanteur soumises à certaines conditions, voir
à
isochrone de Huygens, isochrone
paracentrique, tautochrone,
synchrone
et courbe
de réaction constante.
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2003