Polygonal knot

POLYGONAL KNOT

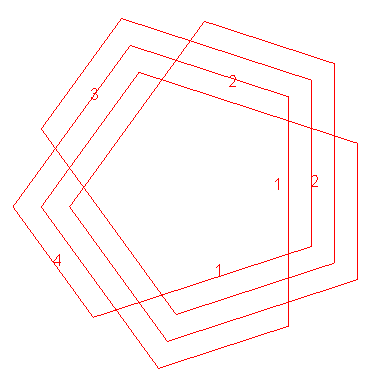
The idea here is to generalize the Scandinavian Valknut represented opposite.
Homemade name.
Figures made by Alain Esculier.

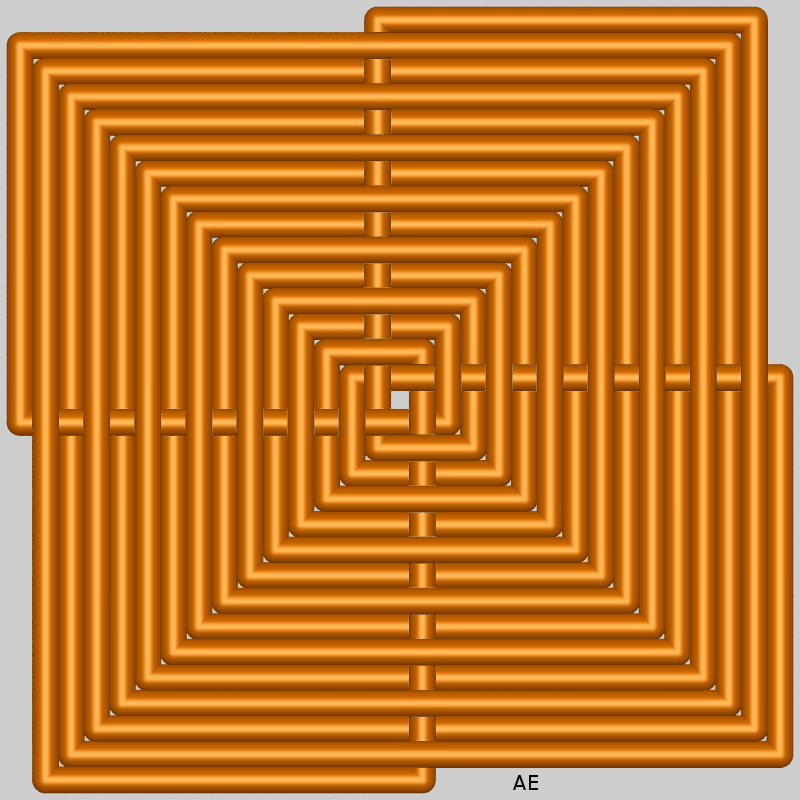
The polygonal knot is constructed as follows: given p regular polygons with n concentric sides as indicated on the figure (for which n = 5, p = 4), we begin on the side of polygon #1, then we go to #2, #3,..., #n, then we come back to #1, and so on, with, no more precisions needed, alternate above/below passages.
If n and p are coprime, we get a polygonal line with np segment lines turning p times around the center, which yields a knot with crossings, trivial if p = 1.
We get the toric knot of type (n, 2) if p = 2, and more generally, the Turk's head of type (n,p).
If the gcd of n and p is d, then there are only p/d turns around the center, which gives a polygonal line with np/d segment lines. But if we rotate d times of a dth of a turn this polygonal line, we get a link with d components and crossings, which is none other than the Turk's head of type (n,p).

Case n = 3:

p = 2, d = 1, N = 3: trefoil knot p = 3, d = 3, N = 6: Borromean ring p = 4, d = 1, N = 9: Turk's head of type (3,4), prime knot 9.1.40 p = 5, d = 1, N = 12, Turk's head of type (3,5).

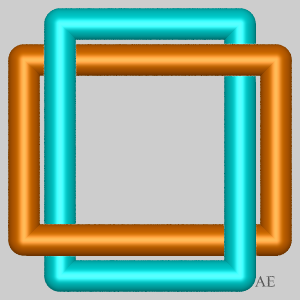
Case n = 4:

p = 2, d = 2, N = 4: Hopf link p = 3, d = 1, N = 8: Turk's head of type (4,3), prime knot 8.1.18 p = 4, d = 4, N = 12: Turk's head of type (4,4), link with 4 loops each loop being interlaced with every other loop. p = 5, d = 1, N = 16: Turk's head of type (4,5), knot with 16 crossings.

Case n = 5:

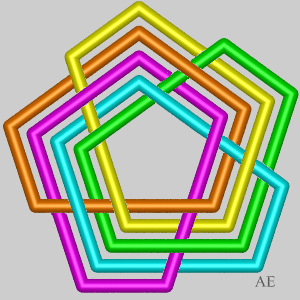p = 2, d = 1, N = 5: toric knot (5, 2). p = 3, d = 1, N = 10: Turk's head (5,3), prime knot 10.1.123 p = 4, d = 1, N = 15: Turk's head (5,4), prime knot with 15 crossings p = 5, d = 5, N = 20: Turk's head (5,5), Brunnian link with 5 loops.

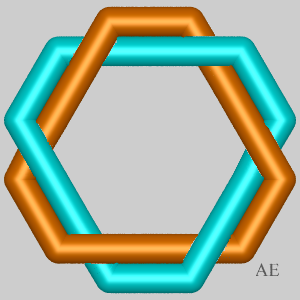
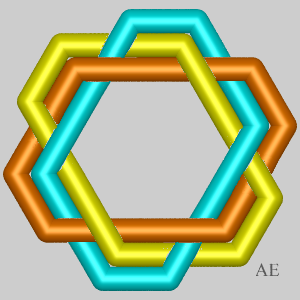
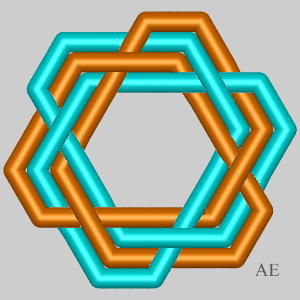
Case n = 6:

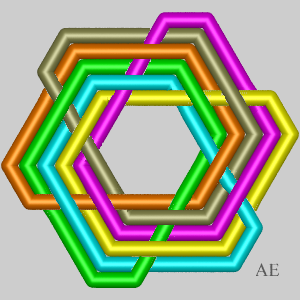p = 2, d = 2, N = 6: toric link (6, 2). p = 3, d = 3, N = 12: Turk's head (6,3), Brunnian link with 3 loops. p = 4, d = 2, N = 18: Turk's head (6,4), link composed of two interlaced trefoil knots p = 5, d = 1, N = 24: Turk's head (6,5), prime knot with 24 crossings p = 6, d = 6, N = 30: Turk's head (6,6), link composed of 6 loops interlaced pairwise.

It can be noticed that for p = n, we get a link with pairwise unknotted loops for odd values of n, and a link with pairwise interlaced loops for even values of n.

next curve previous curve 2D curves 3D curves surfaces fractals polyhedra


p = 2, d = 1, N = 3: trefoil knot	p = 3, d = 3, N = 6: Borromean ring	p = 4, d = 1, N = 9: Turk's head of type (3,4), prime knot 9.1.40	p = 5, d = 1, N = 12, Turk's head of type (3,5).


p = 2, d = 2, N = 4: Hopf link	p = 3, d = 1, N = 8: Turk's head of type (4,3), prime knot 8.1.18	p = 4, d = 4, N = 12: Turk's head of type (4,4), link with 4 loops each loop being interlaced with every other loop.	p = 5, d = 1, N = 16: Turk's head of type (4,5), knot with 16 crossings.


p = 2, d = 1, N = 5: toric knot (5, 2).	p = 3, d = 1, N = 10: Turk's head (5,3), prime knot 10.1.123	p = 4, d = 1, N = 15: Turk's head (5,4), prime knot with 15 crossings	p = 5, d = 5, N = 20: Turk's head (5,5), Brunnian link with 5 loops.


p = 2, d = 2, N = 6: toric link (6, 2).	p = 3, d = 3, N = 12: Turk's head (6,3), Brunnian link with 3 loops.	p = 4, d = 2, N = 18: Turk's head (6,4), link composed of two interlaced trefoil knots	p = 5, d = 1, N = 24: Turk's head (6,5), prime knot with 24 crossings	p = 6, d = 6, N = 30: Turk's head (6,6), link composed of 6 loops interlaced pairwise.