Brunnian link

BRUNNIAN LINK

Notion studied by Hermann Brunn in 1892 and by John Milnor in 1954.
Other name: Borromean chain.
Websites:
https://en.wikipedia.org/wiki/Brunnian_link
katlas.org/wiki/Brunnian_link
www.maths.ed.ac.uk/~aar/papers/liangmislow.pdf
www.knotplot.com
www.aesculier.fr
Pictures made with Povray by Alain Esculier.

A link is said to be Brunnian if it is composed of a certain number of loops (each of them unlinked), with none of them being free, but such that removing one of them frees them all.

It was proved in 1987 that no Brunnian link with 3 loops or more can be made using only circles (see Aigner, Ziegler, Proofs from the book 5th edition p. 95 to 102) .

Examples:
    - any untrivial link with two loops is Brunnian.
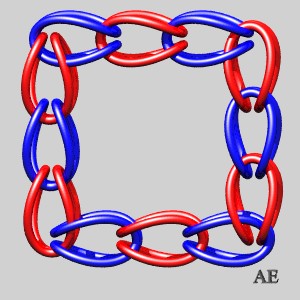
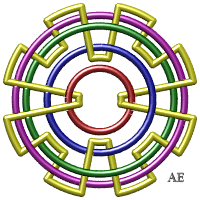
    - The closed link composed of double U-shaped loops in the image in the header shows that there exists a Brunnian link with any given number of loops.
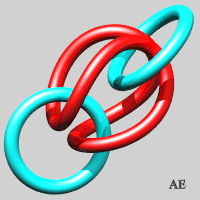
    - We can make an unclosed version of the previous link, on the condition that two blocking rings are placed at the ends; the first step is none other than the Borromean link:

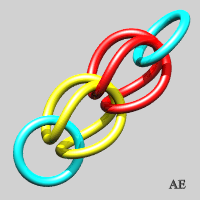
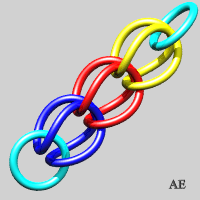
- We can flatten these rings (see on Alain Esculier's website an animation showing the equivalence between the two sequences):

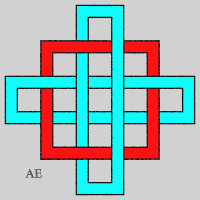
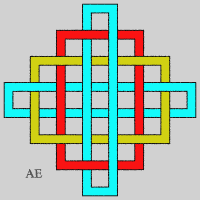
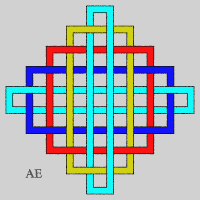
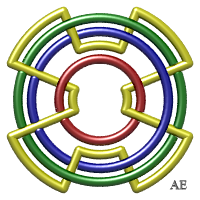
- We get another sequence of Brunnian links with n-components by placing n – 1 concentric circles and intertwining them thanks to a n-th component so that, taken as a whole, the components are intertwined, but form a Brunnian link.
The figure has crossings (number greater than 8n which corresponds to the figure in the header, for n greater than or equal to 5), but it is not the minimal number of crossings. The case n = 3 gives the Borromean link.

- To make a Brunnian link with 3 loops, place two loops on top of one another and make the third one go above the topmost one and below the bottommost one; this does not lead to a unique kind of link: for example, an infinite family of links of this type is composed of the Turk's head knots of type (3x3n) (hence also of the linked polygrams of type {3n/3}), which have 6n crossings.
Not that in the examples below the red loop is above the blue one, which is above the yellow one, which is above the red one...

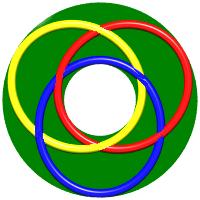
Type (3x3): it is the Borromean link. Type (3x6): 12 crossings
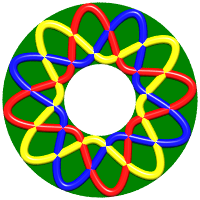
see a carved example at the bottom of the page. Type (3x9): 18 crossings Type (3x12): 24 crossings

Unfortunately, the Turk's heads of type (pxpn), with a number of components p > 3 and with up/down alternating crossings, are not Brunnian (hence neither are the linked polygrams of type {pn/p}). When p is odd, the components are still pairwise untied.

Opposite, the cases (5x5), (7x7) and (5x15): if the components are numbered 1, 2,.., n clockwise, and , then x is below y if y – x is odd, and above y if y – x is even.
Any group of 3 consecutive components thus forms a Borromean link, and is therefore linked.
On the contrary, certain trios such as 1,2,4 are trivial.
See a polygonal version on this page.

When p is even, the situation is even "worse" since all the components are linked to one another (figure on the left).
In the case (4x4), we can improve things by modifying the crossings: in the figure on the right, clockwise, each component is below the next one, green is below blue, and red is below yellow. Among the 4 trios, one of them is trivial (red blue yellow) and the 3 others are Borromean, therefore linked.

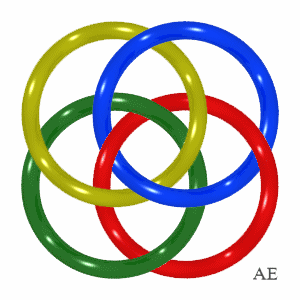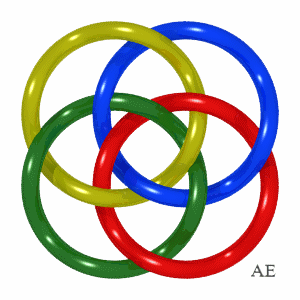
But here is an example of a Brunnian link with 4 loops discovered by Brunn himself in 1892.
Note that contrary to appearances, the rings are not planar.
Do check that any group of 3 rings is composed of 3 free rings, but that each ring is tied by the other three.

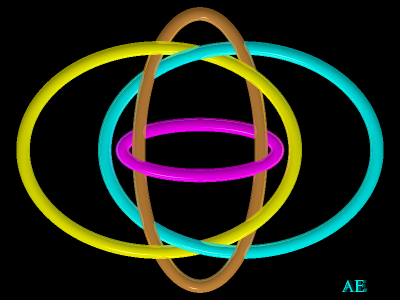In the following we present some "almost"-Brunnian - though not Brunnian - examples.

5 loops, 1, 2, 3, 4, 5; counterclockwise: 1 is below 2, 2 is below 3, 3 is below 4, 4 is below 5, 5 is below 1; moreover, 1 is below 3 and above 4, and 2 is below 4 and above 5, 3 is below 5.
All pairs are untied, the trio 1-2-3 is untied, but the trio 1-2-5 is linked...

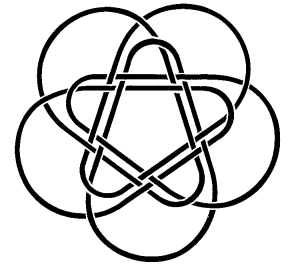Same phenomenon for this 5-loop link called Borromean cross.
Starting from the top, we call the loops 1, 2, 3, 4 and we call 5 the central loop.
1 and 3 are below 2 and 4, 5 is below 1 and 3, and above 2 and 4.
All the pairs are untied, the 4 external trios and the 2 cross trios are trivial, but the 4 trios that include the central loop are Borromean links, and therefore are linked.
All the quartets are linked.

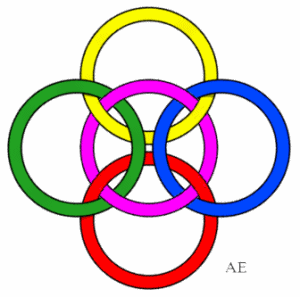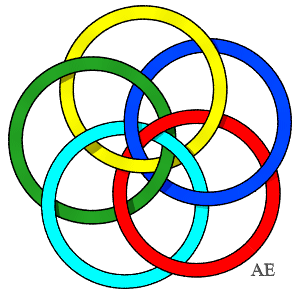
Another 5-loop link.
All the pairs are untied, the 5 trios of consecutive rings are trivial, but the other 5 are Borromean. Therefore, this link is not equivalent to the previous one.

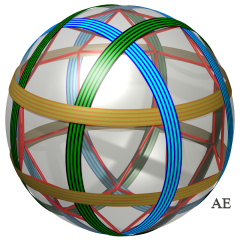
This 6-loop link is associated to the rhombicuboctahedron. It can be obtained by considering a second copy of the three Borromean loops associated to the octahedron.
Each of the 8 tricolor trios of circles form a trio of Borromean rings, and is therefore linked.
However, if we cut two loops of the same color, the whole is freed.

Headstones in Turkey.
The first one comes from the Bodrum Castle: it is an alternating Turk's head knot of type (3x6) which is indeed Brunnian.
The second one comes from the archaeological museum of Milas. Non alternating, the loops are linked pairwise.

next curve previous curve 2D curves 3D curves surfaces fractals polyhedra

Type (3x3): it is the Borromean link.	Type (3x6): 12 crossings see a carved example at the bottom of the page.	Type (3x9): 18 crossings	Type (3x12): 24 crossings

5 loops, 1, 2, 3, 4, 5; counterclockwise: 1 is below 2, 2 is below 3, 3 is below 4, 4 is below 5, 5 is below 1; moreover, 1 is below 3 and above 4, and 2 is below 4 and above 5, 3 is below 5. All pairs are untied, the trio 1-2-3 is untied, but the trio 1-2-5 is linked...
Same phenomenon for this 5-loop link called Borromean cross. Starting from the top, we call the loops 1, 2, 3, 4 and we call 5 the central loop. 1 and 3 are below 2 and 4, 5 is below 1 and 3, and above 2 and 4. All the pairs are untied, the 4 external trios and the 2 cross trios are trivial, but the 4 trios that include the central loop are Borromean links, and therefore are linked. All the quartets are linked.
Another 5-loop link. All the pairs are untied, the 5 trios of consecutive rings are trivial, but the other 5 are Borromean. Therefore, this link is not equivalent to the previous one.
This 6-loop link is associated to the rhombicuboctahedron. It can be obtained by considering a second copy of the three Borromean loops associated to the octahedron. Each of the 8 tricolor trios of circles form a trio of Borromean rings, and is therefore linked. However, if we cut two loops of the same color, the whole is freed.