BADERNE D'APOLLONIUS et EMPILEMENT APOLLONIEN
Apollonian gasket and apollonian packing, apollonische
Kreise und apollonische Verpackung

| fractal suivant | fractal précédent | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
BADERNE D'APOLLONIUS et EMPILEMENT APOLLONIEN
Apollonian gasket and apollonian packing, apollonische
Kreise und apollonische Verpackung


| Objet ainsi nommé en l'honneur d'Apollonius qui
est supposé avoir résolu le problème de la détermination
des cercles tangents à 3 cercles (vers 200 avant J.C), dans son
ouvrage disparu "le traité des contacts". La première apparition
du terme baderne d'Apollonius semble être due à François
Apéry en 1982.
Une baderne est un tapis tressé avec de vieux cordages
; il faut imaginer probablement ici la section droite d'un cordage, qui
fait apparaître des cercles tangents.
Sites web :
|

 |
La baderne d'Apollonius est un fractal construit de la
façon suivante :
| Étant donné un triangle (ABC), il existe exactement 3 cercles 2 à 2 tangents centrés en A,B,C (de rayons respectifs (–a+b+c)/2, (a–b+c)/2, (a+b–c)/2). |
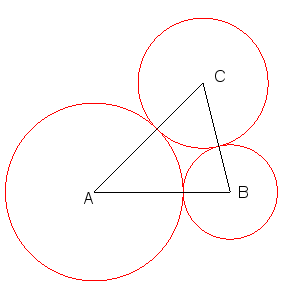 |
| Il existe alors un unique cercle tangent aux trois cercles
précédents et intérieur au triangle, appelé
(petit) cercle de
Soddy du triangle (ABC) (un deuxième cercle tangent aux
trois cercles est situé à l'extérieur du triangle).
Son centre S est à l'intersection des 3 arcs d'hyperboles MA–MB=b–a, MB–MC=c–b, MC–MA=a–c, tracés en vert ci-contre. Son rayon est donné par la belle relation de Descartes (1643) : S se calcule par la relation de Descartes complexe : |
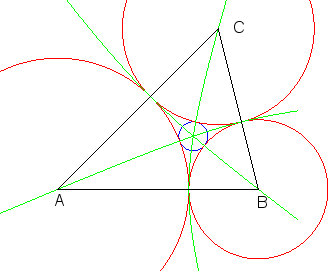 |
| Le point de Soddy S détermine 3 nouveaux triangles (SAB), (SBC), (SCA), qui ont eux-même un cercle de Soddy, en mauve ci-contre. | 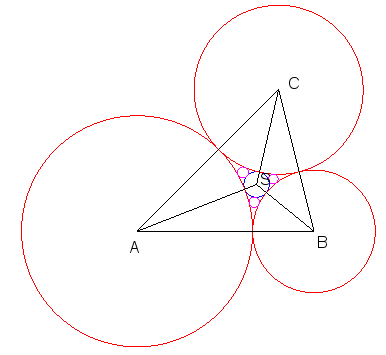 |
| Chacun de ces 3 triangles est de nouveau découpé
en 3 triangles ayant chacun un cercle de Soddy, en bleu ciel ci-contre
; à cette troisième étape nous avons 1+3+9 = 13 cercles
de Soddy.
En réitérant le procédé, nous
aurons à la n-ième étape |
 |
|
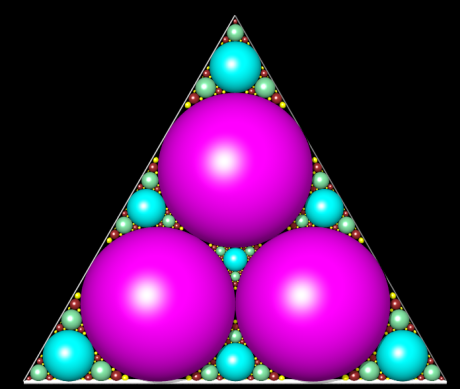
La baderne d'Apollonius est la figure formée de tous ces cercles lorsque n tend vers l'infini. Plus précisément, l'ensemble fractal est l'adhérence de la réunion de ces cercles. C'est un fractal en ce sens que la baderne d'Apollonius associée au triangle (ABC) est la réunion des 3 badernes associées aux triangles (SAB), (SBC), (SCA) (la construction est d'ailleurs similaire à celle du triangle de Sierpinski, qui est formé de 3 triangles semblables). Sa dimension fractale, beaucoup moins simple à calculer que celle du triangle de Sierpinski, est d'environ 1,3057. Ci-contre, la baderne à la 5ème étape ; remarquer la différence de taille des cercles de la cinquième étape, dont certains ne se distinguent déjà plus. |
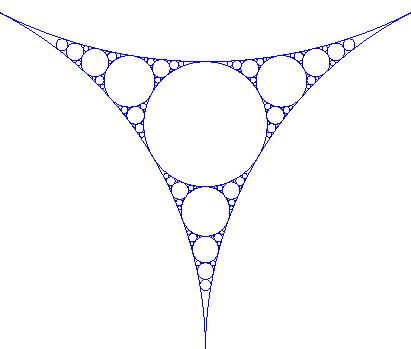 |
| On désigne aussi par baderne d'Apollonius une
figure légèrement différente utilisant le fait que
3 cercles deux à deux tangents (intérieurement ou extérieurement)
possèdent toujours exactement deux cercles qui leur sont tangents.
On débute avec trois cercles tangents C1, C2 et C3 qui ont deux cercles tangents C4 et C5. On a donc 6 nouveaux triplets de cercles tangents qui ont chacun deux cercles tangents, mais l'un de ces deux cercles est l'un des cercles de départ C1, C2 ou C3. La figure montre les 3 cercles de départ en rouge, les 2 cercles tangents de la première étape en bleu, et les 6 cercles tangents de la deuxième étape en vert. |
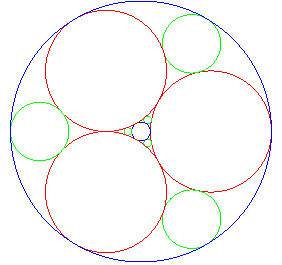 |
| En réitérant ce procédé,
nous aurons à la n-ième étape Ci-contre les 29 cercles de la troisième étape. |
 |
| La baderne à la cinquième étape.
La figure limite est aussi l'ensemble limite des 4 inversions dont les cercles sont tracés en noir. Remarquer que l'intersection de la baderne avec l'intérieur d'un cercle noir a pour inverse par rapport à ce cercle le reste de la baderne ! |
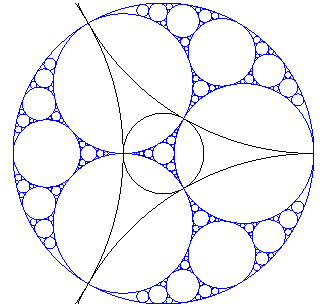 |
Plus généralement, étant donné un compact connexe quarrable K du plan, on désigne par empilement apollonien de K toute famille de disques fermés disjoints ou tangents inclus dans K, chaque disque étant tangent à au moins trois autres, et l'empilement est dit complet si le complémentaire dans K de la réunion des disques est d'intérieur vide (ou, ce qui est équivalent, que la somme des aires des disques de la famille est égale à l'aire de K).
Il n'a été démontré
qu'en 1943 que les disques fermés de la baderne d'Apollonius
premier type forment un empilement apollonien complet de la "deltoïde"
(ou triangle curvinigne) formée par les 3 cercles tangents de départ,
ou que la baderne deuxième type forme un empilement apollonien complet
du grand disque.
Et il a été démontré en 1973
que tous les empilements apolloniens complets ont la même dimension
fractale, donc celle indiquée ci-dessus.
| On obtient un empilement apollonien complet de K
par l'algorithme "glouton" suivant :
Il existe un disque fermé de rayon maximal inclus dans K (non forcément unique, par exemple pour le rectangle). Si le rayon de ce disque est non nul, on réitère cette opération avec toutes les composantes connexes du complémentaire de l'intérieur du disque maximal, et on réitère ce procédé à l'infini. Ci-contre, voici ce que cela donne pour le triangle : |
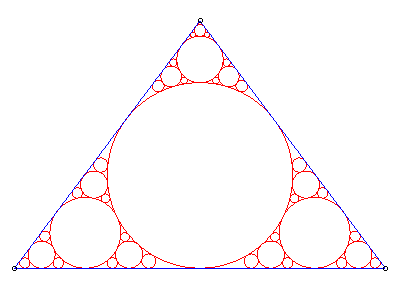 |
| Programme Maple de construction de la baderne (du premier type))
restart:with(plots):dist:=(A,B)->sqrt((A[1]-B[1])^2+(A[2]-B[2])^2): #========= détermine les cercles 2 a 2 tg centrés en A,B,C ====== initBaderne:=proc(A,B,C) local a,b,c: a:=dist(B,C);b:=dist(C,A);c:=dist(A,B); [A,(-a+b+c)/2],[B,(a-b+c)/2],[C,(a+b-c)/2]: end: #-----détermine le petit cercle de Soddy de ABC soddy:=proc(A,B,C) local a,b,c,d,r1,r2,r3,a1,b1,c1,d1,x1,x2,x3,y1,y2,y3,x,y,r; a:=dist(B,C);b:=dist(C,A);c:=dist(A,B); r1:=(-a+b+c)/2:r2:=(a-b+c)/2:r3:=(a+b-c)/2: r := (r1*r2*r3)/(r1*r2+r2*r3+r1*r3+2*sqrt(r1*r2*r3*(r1+r2+r3))): x1:=A[1]:y1:=A[2]:x2:=B[1]:y2:=B[2]:x3:=C[1]:y3:=C[2]: a,a1 := 2*(x1-x2),2*(x1-x3):b,b1 := 2*(y1-y2),2*(y1-y3):c,c1 := 2*(r1-r2),2*(r1-r3): d,d1 := (x1^2+y1^2-r1^2)-(x2^2+y2^2-r2^2),(x1^2+y1^2-r1^2)-(x3^2+y3^2-r3^2): x := (b1*d-b*d1-b1*c*r+b*c1*r)/(a*b1-b*a1): y := (-a1*d+a*d1+a1*c*r-a*c1*r)/(a*b1-b*a1): [[x,y],r] end: #--------algorithme récursif de construction de la baderne----------- baderne:=proc(CA,CB,CC,n) local CS; if n=0 then NULL else CS:=soddy(CA[1],CB[1],CC[1]): {CA,CB,CC} union baderne(CA,CB,CS,n-1)union baderne(CB,CC,CS,n-1)union baderne(CC,CA,CS,n-1) fi; end: traceListe:=proc(L,col) plot({seq([L[i,1,1]+L[i,2]*cos(t),L[i,1,2]+L[i,2]*sin(t),t=0..2*Pi],i=1..nops(L))},color=col) end: A,B,C:=[-1.,0],[1.,0],[0,sqrt(3.)]:deb:=initBaderne(A,B,C):fig:=baderne(deb,4): display(traceListe(fig,blue),axes=none,view=[-0.51..0.51,0..0.86],scaling=constrained); |
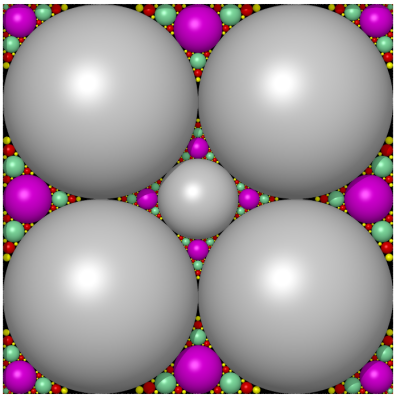
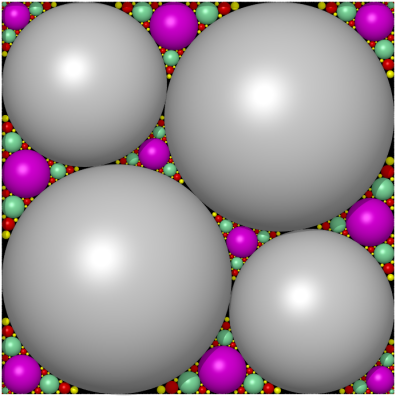
Empilements apolloniens du carré, par Alain Esculier, les disques
étant remplacés par des sphères.
L'algorithme glouton est mis en oeuvre en partant d'un empilement quelconque
(en gris).
Première étape en mauve, deuxième en magenta,
troisième en vert d'eau, quatrième en rouge, cinquième
en jaune....
Voir d'autres empilements apolloniens sur son
site.


Rosace de la cathédrale de Strasbourg, de l'abbaye
des Vaux de Cernay
| fractal suivant | fractal précédent | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL , Alain ESCULIER 2014