fractal suivant fractal précédent courbes 2D courbes 3D surfaces fractals polyèdres

ARBRE FRACTAL
Fractal tree, Baum-Fraktal

Code maple récursif pour calculer l'arbre ci-dessus proc_arbre:=proc(A,B,L,t,n)
local k,M;
  k:=nops(L):
  M:=evalf([seq(L[q]*exp(t[q]*I),q=1..k)]);
  if n>0 then [A,B],seq(proc_arbre(B,B+M[q]*(B-A),L,t,n-1),q=1..k)
  else [A,B] fi
end:
arbre:=[proc_arbre(0,I,[0.7,0.7],[Pi/9,-2*Pi/9],9)]:
arbre:=map(y ->map(x ->[Re(x),Im(x)],y),arbre):
Affichage en 2d plot(arbre,axes=none,color=COLOR(RGB,0.55,0.2,0),scaling=constrained);
Affichage en 3d tube:=proc(A,B,q,n)
  tubeplot([(1-t)*A[1]+t*B[1],(1-t)*A[2]+t*B[2],0],t=0..1,radius=(2-t)*0.1/(1+q),grid=[2,20],color=COLOR(RGB,(1-q/n)*.55,(1-q/n)*.2+q/n*0.7,0.05))
end:
affiche3d:=proc(arbre,n)
 local LL,i :
 LL:= [seq(i,i=1..n+1 )]:for i from n+1 to 2 by (-1) do LL:=[op(LL),op(LL[i..nops(LL)])] od;
 display3d(seq(tube(arbre[k][1],arbre[k][2],LL[k],n),k=1..nops(arbre)),scaling=constrained,style=patchnogrid,lightmodel=light2,orientation=[-90,0]);
end:
affiche3d(arbre,9);
© Robert FERRÉOL, Alain ESCULIER 2002

Un arbre est fractal en ce sens que ses branches maîtresses, issues du tronc, sont chacune des arbres en réduction. Pour simplifier, si le tronc est le segment [AB], nous allons considérer p similitudes fi transformant le segment [AB] en des segments plus courts [CiDi], attachés aux troncs (c'est-à dire que Ci appartient à [AB]). Remarquons qu'il y a exactement deux similitudes possibles pour chaque [CiDi], l'une directe, l'autre indirecte.
Partant de K0  = [AB], on définit la suite des compacts , qui converge vers l'attracteur des fi , lequel peut être considéré comme le "feuillage" de l'arbre :

Feuillage de l'arbre ci-dessus
L'arbre est, lui, la réunion des Kn ; son feuillage est donc l'ensemble des extrémités de ses branches.

Voici la construction animée des 10 premières étapes, avec des Ci égaux à B, et deux similitudes directes de rapport 0,7 et d'angles p/9 et -2p/9.


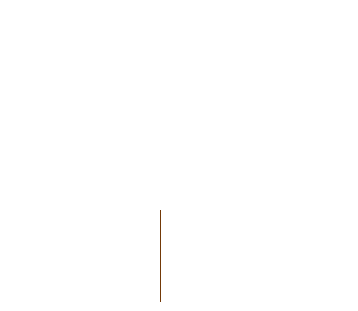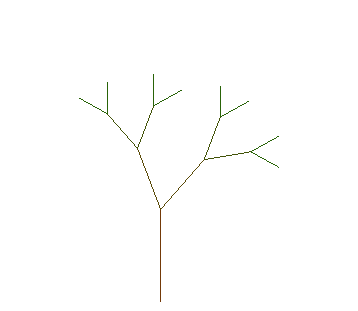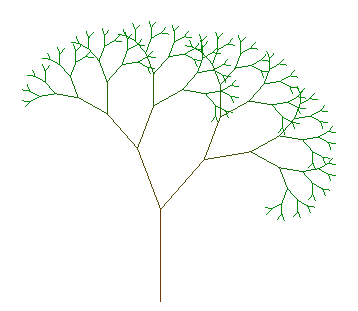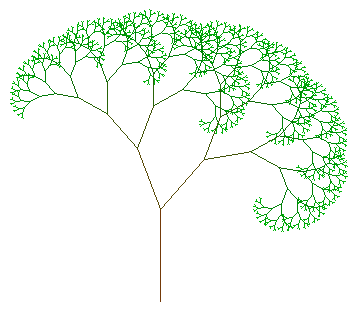
Remarquons que l'arbre est formé de spirales logarithmiques approchées :  et 

Si l'on veut obtenir l'arbre complet comme un attracteur, il faut rajouter une p + 1ème contraction. Certains auteurs prennent une affinité de rapport assez petit de façon à ramener l'arbre au tronc. Ceux qui considèrent qu'assimiler le tronc à un arbre en réduction est une imposture peuvent aussi prendre une fonction qui donne un point choisi au hasard dans le segment [AB], ou mieux, dans un rectangle de médiane ce segment, pour obtenir une épaisseur. Cette fonction n'est alors plus une contraction à proprement parler, ce qui n'empêche pas l'algorithme de très bien fonctionner :

Si l'on prend des similitudes directes de rapport 1/2 et d'angles , 0 et , C1 = milieu(A,B) , C2 = B, C3 = milieu(C1,B), on obtient l'érable :

Un beau sapin est obtenu avec 4 similitudes directes de rapports 1/2, 1/2, 1/3 et 2/3 et d'angles , , 0 et 0, C1 = C2 = C3 = A ,  C4 =(2A + B)/3 :
 

Encore plus vraisemblable avec une affinité.

Le feuillage de ce sapin, avec un angle de p/4 au lieu de p/6.

Voici un arbre taillé en espalier (2 similitudes directes de rapport 0,7 et d'angles , , C1 = C2 = B) :

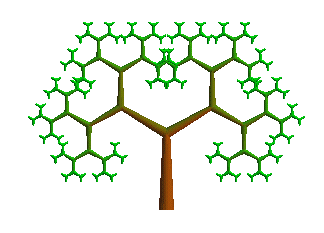
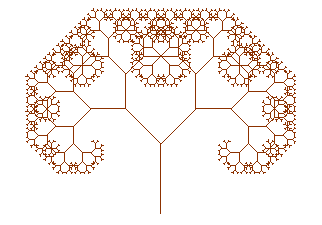
L'arbre suivant obtenu par 2 similitudes directes de rapport 1/Ö2 et d'angles , , C1 = C2 = B est encore moins naturel :

mais il possède la particularité d'avoir un feuillage égal à la courbe du C ;
Le feuillage de cet arbre est donc connexe ; lorsque c'est le cas, on parle de canopée (terme qui désigne, dans le civil, le dôme compact de la forêt vierge).

Avec deux similitudes d'assez faible rapport (1/4) et une similitude de rapport assez proche de 1 (0,85) et de faible angle, on obtient une fougère :  Ici, c'est une vue de l'étape 6, mais il faudrait aller au moins jusqu'à l'étape 30 pour en obtenir tous les étages distingables, ce qui est impossible (330 = 2. 1014 segments...) ; voir la suite à l'article fougères.

L'arbre suivant, à branches d'épaisseur variable, a été dénommé "arbre de Pythagore" car il est formé de copies de la figure classique illustrant le théorème de Pythagore :

Tous les arbres précédents étaient plans, mais voici voici un arbre en 3D, à trois branches également réparties (évidemment reprojeté dans un plan...) :

Voir aussi :
mariefrance.hellot.free.fr/Tree1.html
aesculier.fr/fichiersPovray/arbre3d/arbre3d.html
 

Ca, c'est un vrai !
(dragonnier photographié par Alain Esculier à Tenerife)

Arbre de Pythagore, les carrés étants allongés en rectangles, et les barres intermédiaires supprimées.

 
fractal suivant fractal précédent courbes 2D courbes 3D surfaces fractals polyèdres

© Robert FERRÉOL 2016