CONE

| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
CONE

| Cartesian equation of a cone with vertex O: f(x,
y,
z)
= 0 with f homogeneous.
In particular: z = f(x, y) with f homogeneous of degree 1. Cartesian parametrization: Cylindrical equation: 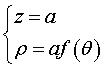 ). ).
Parametrization stemming from the polar coordinates Parametrization with geodesics (other than the generatrices): |
A cone (or conical surface) is a ruled
surface the generatrices of which pass through a fixed point O (its
vertex), in other words, a surface globally invariant under any homothety
centered on O (with ratio 0).
A curve traced on the cone that intersects all the generatrices
is called a directrix of the cone; there exists a unique cone with
given vertex and directrix.
An algebraic surface with equation f(x,y,z)
= 0 is a cone with vertex O if and only if the polynomial f
is homogeneous. The degree of f is then the degree of the
cone (as an algebraic surface).
The sections of this cone by planes that do not pass
by O are then the various curves (projectively equivalent) with
homogeneous equation .
Examples:
- cone
of revolution
- elliptic
cone
-
sinusoidal cone
- Cartan's
umbrella
Compare to the conoids.
| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017