RULED SURFACE
A ruled surface (or a scroll) is a surface that
is the union of lines, called its generatrices. A directrix cone
is associated to it, union of the lines passing by a given point and parallel
to the generatrices.
By three curves, there passes in general a unique ruled
surface, union of the lines meeting these three curves. If the three curves
are algebraic of respective degrees p,q,r, then the surface is "in
general" algebraic of degree 2pqr.
| The family of lines supported on two given curves does
not generate, in general, a surface; but it is the case if we add another
condition, like: |
The examples below show various ruled surfaces supported
on a semicircle and a half-ellipse: |
| 1) the lines have to meet a third given curve (hence
family of the lines supported on three curves) |
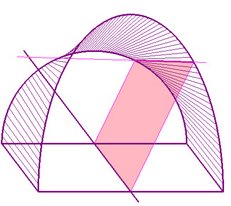
the third curve is a line
|
| 2) they must be parallel to a given "directrix" plane
(Catalan surface) |
|
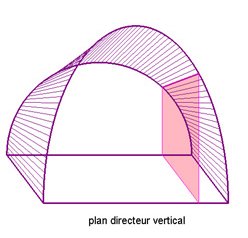
| 3) the surface is developable
(hence the envelope of the family of common tangent planes of the two curves,
such planes being obtained by taking a tangent to a curve, and a tangent
to the other curve, secant to the first tangent) |
|
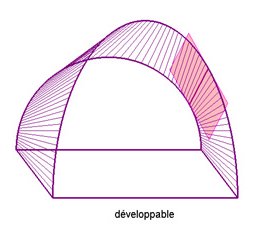
| 4) the distance between two contact points is constant
(see the examples of the milk carton
and the oloid) |
|
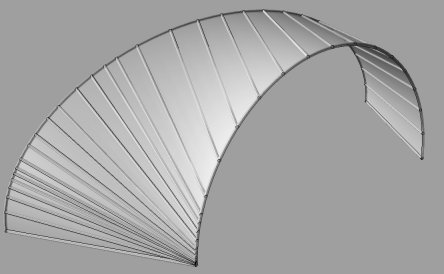
The points of a ruled surface are hyperbolic
or parabolic; when a point is parabolic, all the points on its generatrix
are also parabolic; this happens when it is tangent to the striction
line and corresponds to the case where the distribution parameter is
equal to zero.
Examples:
- the cones, the
cylinders,
and more generally, the developable
surfaces (case where all the generatrices are parabolic).
- the conoids
(including the hyperbolic
paraboloid) and more generally the Catalan
surfaces (planar directrix cone)
- the conoidal
surfaces (including the milk
carton) and more generally the surfaces
with a straight directrix
- the one-sheeted
hyperboloids.
- the right
helicoids (including the right helicoid and the developable helicoid).
- the Möbius
surface and more generally the Cayley
ruled cubics.
- Hector Guimard's
surface.
- examples of Seifert
surfaces.
The ruled non-degenerate quadrics
are the surfaces union of lines meeting three lines two by two non coplanar:
hyperbolic
paraboloid in the case where the three lines are parallel to a fixed
plane and one-sheeted hyperboloid
in the other case; they are the only doubly ruled surfaces (i.e.
that are the union of two distinct families of lines).
The cubic ruled
surfaces are the cones and the cylinders with a cubic as a directrix,
the conoidal surfaces of degree 3 and the Cayley ruled surfaces.
The ruled surfaces of revolution are the one-sheeted
hyperboloids.
See also their cousins, the circled
surfaces.
Fences at La Villette, Paris (2014) |
Catenaries forming elegant ruled surfaces |
© Robert FERRÉOL,
Robert March 2017
.
,
union of the generatrices Du
passing by 
with direction vector 
(more simply: 
);
directrix cone: 
.
.
and left-handed if 
; it is developable iff
d
= 0.
where 
is the distance between Du
and Du+du
and 
is the angle between Du
and Du+du
.