Oloid

OLOID

The general case of the developable circumscribed to two conics was studied by Poncelet, Chasles, Cayley and Jules de la Gournerie in the 19th century, but the oloid itself was studied by Paul Schatz in 1933. According to Georg Unger, the latter had named it "polysomatoloid", according to a new science he had named "polysomatology". But as he thought no one could pronounce it, he shortened it - half jokingly - to "oloid". Another possibility: use of the Greek word "olos" all.
Ref : Paul Schatz, The Study of Rhythms and Technology, p. 13.
Other name: orthobicycle, given in 2004 by Robert March.

The oloid is the convex hull of two orthogonal circles each passing by the center of the other. Its surface is a part of the developable surface supported on the two circles (proof: H. POTTMANN, J. WALLNER : Computational Line Geometry, Springer-Verlag Telos (2001) p. 405)

View of the oloid with the generatrices restricted to the two directrix circles.
The surface is invariant under the action of the two half-turns swapping the two circles and is therefore composed of two symmetric parts, here in red and blue.
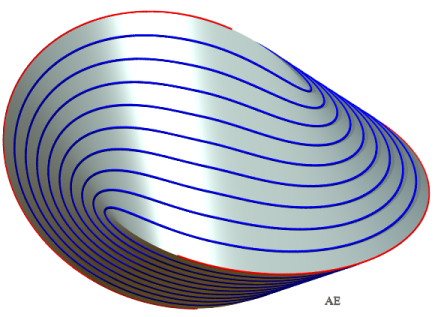
The axes of the half-turns are the two perpendicular lines passing by the middle of the centers of the 2 circles, perpendicular to the axis of the centers, and forming an angle of 45° with the planes of the circles. View of the developable surface of with the generatrices extended, showing the cuspidal edge, composed of 4 branches.

Geometric construction of the generatrices.
The developability condition is that any tangent plane is the same all along the generatrix (MN) (when M describes the first circle and N the second one); the two tangents to the circles at M and N are therefore included in this plane; but each one is also included in the planes of the circles, which intersect at a line (D); the two tangents therefore intersect at a point P on (D), which determines M knowing N and vice versa (besides, this holds for any developable surface supported on two plane curves).

If we choose and , then the relation between u and t is given by . The distance MN is constant, equal to .
Cartesian equation of the surface:
.
Algebraic surface of degree 8.
Volume of the oloid: .
Area of the lateral surface: (= area of the sphere with radius 1)

Two circles rolling on a plane give the pattern of this surface (models made by Robert March):

The oloid can be generalized for 2 perpendicular circles with equal radii but with any distance between the centers. The case where the circles have the same center gives an equidomoid, union of 4 portions of elliptic cylinders.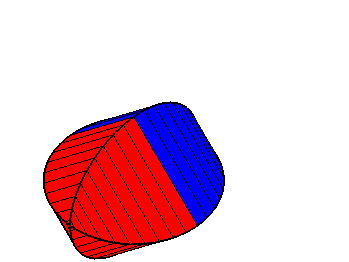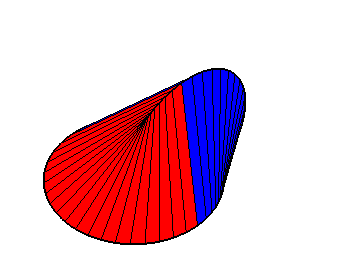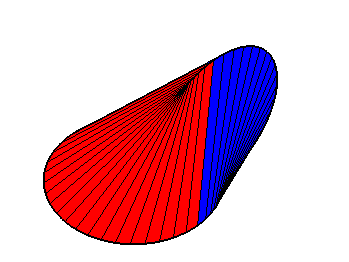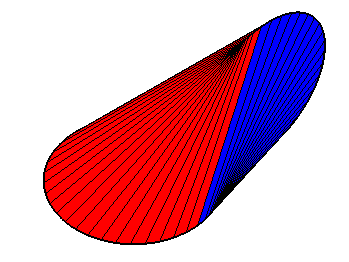
Paper models made by Yves Maniette

Do not mistake the oloid for the sphericon, which is the convex hull of two perpendicular half circles with same the same center. Its surface is also developable since it is composed of 4 portions of cones of revolution that connect "tangentially", but with curvature discontinuities.
Also note that the edges are two semicircles whereas those of the oloid are larger portions of circles.

Links:
Mathematical study of the oloid (with, among other things, the parametrization of the curve limiting the development of the oloid)
Website on the oloid in German
Physics, toys and art

Oloid made by Robert March's students

Oloid, sculpture by Roland de Jong Orlando

next surface previous surface 2D curves 3D curves surfaces fractals polyhedra