DEVELOPABLE SURFACE
| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
DEVELOPABLE SURFACE

| Notion studied by Leonhard
Euler in 1777 and Gaspard Monge in 1775/80.
Other names : torse, torsal surface, flat surface. See this article by Etienne Ghys and this Swedish website. |
| Partial differential equation for an explicit surface
z
= f (x, y) (Monge notations):
rt =
s²
(all the points are parabolic).
For an implicit surface f(x,y,z)=0: For a ruled surface (S) union of the lines Du : 1) If the lines Du
are defined by a point Special case First fundamental quadratic form: 2) The set of lines |
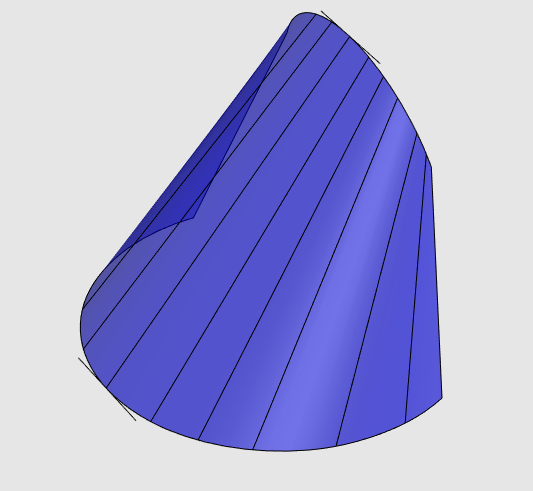
A developable surface (or torse) is a ruled surface that can roll without slipping on a plane, the contact being along a line, similarly to a cylinder or a cone. Concretely, it is a surface that is obtained by deforming without folding a sheet of cardboard.
The following definitions characterize the developable surfaces:
DEF 1: a developable surface is a ruled surface for which
any generatrix is stationary, i.e. such that the tangent plane of the surface
is the same at any point of the generatrix.
Directly equivalent conditions:
- 1.1 ruled
surface for which the generatrices are parabolic.
- 1.2 ruled surface such that the
principal normal along a generatrix generates a plane;
- 1.3 ruled surface the generatrices
of which are curvature
lines (see
normal surface).
- 1.4 ruled surface such that the
planes parallel to the tangent planes passing by a given point envelope
the directrix cone of the surface (union of the lines parallel to
the generatrices passing by the point).
DEF 2: A developable surface is a surface for which every generatrix intersects with the generatrices infinitely close (cf. above Du and Du+du intersect), possibly at infinity (case of the cylinders).
DEF 3: a developable surface is a ruled surface the generatrices of which have an envelope (possibly reduced to a point (case of the cones), or even a point at infinity (case of the cylinders)).
DEF 4: a developable surface is a cone, a cylinder, or the surface generated by the tangents of a 3D curve (or, which amounts to the same thing, the envelope surface of the osculating planes of the curve); this curve is the cuspidal edge of the surface.
DEF 5: a developable surface is the envelope surface of a family of plane with one parameter.
DEF 6: a developable surface is the polar developable of a skew curve (i.e. the envelope of the normal planes); the skew curve is then an involute of the surface.
DEF 7: a developable surface is the envelope surface of
the rectifying plane of a 3D curve (planes containing the tangent
and binormal vector); the skew curve is then a geodesic
of the surface and the surface is called rectifying developable (or
torse) of this curve; the generatrix passing by M (the rectifying
line) supports the instant rotation vector of the Frenet frame ;
the point of the cuspidal edge is
.
DEF 8: a developable surface is a Monge surface with a linear generatrix (surface generated by the movement of a fixed line on a moving plane all the points of which have a speed vector orthogonal to this plane).
They are the surfaces all the points of which are parabolic (i.e. with zero total curvature or also such that one of the principal curvature radii is infinite); what is remarkable, is that, conversely, any surface without planar point for which all the points are parabolic is included in a developable surface.
The developable surfaces are surfaces applicable
to the plane, and conversely, any surface of class C2
applicable
to the plane is included in a developable surface. When a surface is applied
onto the plane, it is said to be developed.
The class C2 condition
is important because we can construct non ruled surfaces of class C1
applicable
to a plane; it is said that when Darboux stated in a lecture at École
normale supérieure at the end of the 19th century that "any developable
surface is a ruled surface", the student Henri Lebesgue took out his handkerchief
and said: "Show me the generatrices!" (cf Berger p. 148).
When a developable surface with a cuspidal edge rolls on a plane, the trace of the edge is a curve that has the same relation between the curvilinear abscissa and the curvature (but without torsion) and the tangents are applicable onto one another; inversely, this allows to see a developable surface as the result of the torsion of a plane curve along with its tangents.
Examples:
- the cones
- the cylinders,
- the developable
helicoid (the cuspidal edge of which is a circular helicoid, result
of the torsion of a circle), and
- more generally, the surfaces
of equal slope.
- the tangent
developable of the skew parabola.
- the developable
Möbius strip
- the oloid
See also normal surface.
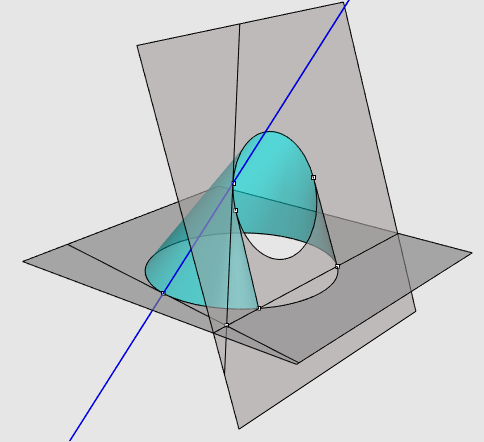
| There is usually a single developable surface containing
two given curves
: the envelope of the tangent planes common to both curves. The condition of existence is that any tangent to the first curve is secant to a tangent to the second curve, and vice versa(so no developable surface relying on two non-coplanar lines, for example). This condition is for example realized if the two curves are located in two secant plans (and that their tangents have all possible directions in these plans). Opposite, figure duced to Robert March, construction in
the case of two
The apparent outline of the surface is rectilinear, property
|
 |
| If the two curves are parallel, the developable surface is the reunion of the lines perpendicular to the two curves. For example, if we extend the ties of these roller coaster tracks, we obtain two developable surfaces. |  |
| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2019