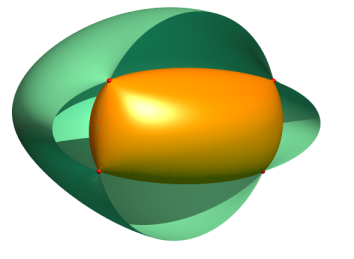
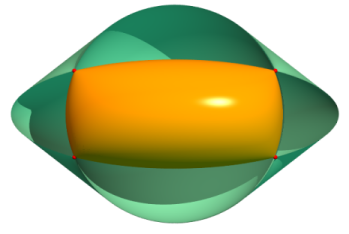
Cartesian equation:  where , for the ellipsoid ,  or , i.e.. Cartesian parametrization: . Quartic surface.

Fresnel's wave surface is derived from the ellipsoid in the following way: for any plane passing through the center O, write down the semi-axes of the ellipse section of the ellipsoid by this plane, and mark these lengths on the normal at O of this plane, starting from O (which makes 4 points). The wave surface is the locus of these four points.

The above equation comes form the fact that the semi-axes of the section of the ellipsoid by the plane  are the solutions of the equation with unknown k: .
 
 

For , the surface is formed of an outer shell and an inner part that meet to the four singular points .

The wave surface construction method was generalized for any surface: given a surface and a point O, for any plane passing by O, write down the "apsis radii" with respect to O of the section of the surface by this plane, i.e. the maximal or minimal distances from a point on the curve section to O, and mark these lengths on the normal at O of the plane, starting from O. The surface obtained is called the apsis surface with respect to O of the initial surface.
For example, the apsis surface of a plane with respect to a point O is the cylinder perpendicular to the plane with axis passing by O and radius the distance from O to the plane.
The apsis surface of a sphere with respect to a point O is a torus with axis the line joining O to the center of the sphere, major radius the distance from O to the center of the sphere, and minor radius the radius of the sphere.
 

The wave surface is called this way because it is the locus of the ends of various wave rays emitted by a source placed at O in a birefringent medium, during a given time.

See also Fresnel's elasticity surface.
 
 

next surface

previous surface

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL   2017