Curve studied by Leibniz in 1687 and by Jacques Bernoulli in 1690. Wilhelm Gottfried Leibniz (1646 - 1716): German philosopher and scholar.

 

With Ox as the descending vertical axis and a starting point at O with zero horizontal speed, the conservation of energy gives , i.e.  since . Hence the kinematics equations of motion:  that can be integrated to: , hence the equation of the trajectory: .

An isochronous curve of Leibniz is a curve such that if a particle comes down along it by the pull of gravity, the vertical component of the speed is constant, when the gravitational field is supposed to be uniform.

The solution is a semicubical parabola, as shown in the above derivation. Note that the initial speed at the vertex of the parabola must be equal to  for the semicubical parabola  to be isochronous; the vertical component is then a constant equal to (and the horizontal component is proportional to the square root of time).

The particle descends along this curve this constant vertical speed
Attention! for a given curve (and given gravity), there is only one possible initial speed for the phenomenon to occur

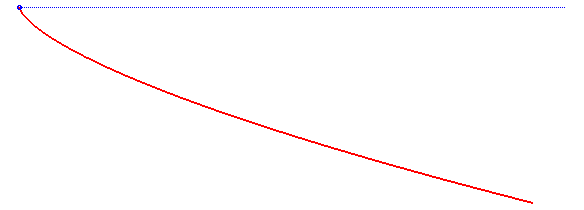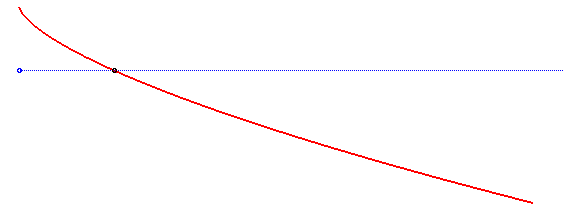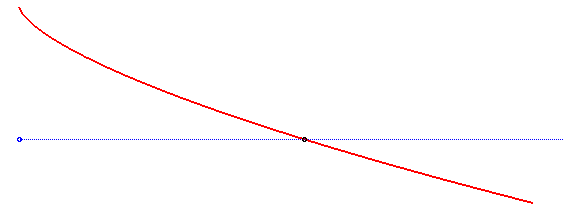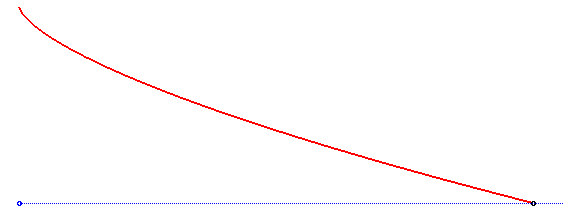
In this derivation, the acceleration vector of the gravity force was supposed to be constant; if it is only supposed to have constant norm, but is oriented in the direction of a point at finite distance, then we get the curves called isochronous curves of Varignon.

For other curves of motions of a massive point in a gravitational field subject to certain conditions, see the isochronous curves of Huygens, the paracentric isochronous curve, the tautochronous curves, the synchronous curves and the curve of constant reaction.
 

next curve

previous curve

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL  2017