CURVE WITH CONSTANT REACTION, L'HOSPITAL QUINTIC

The force applied by the marble on the support is constant
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
CURVE WITH CONSTANT REACTION, L'HOSPITAL QUINTIC

The force applied by the marble on the support is constant
| Problem of the "curva aequabilis pressionis" posed by
Jean Bernoulli in 1695, solved by L'Hospital in 1700.
Other names: curve with constant pressure, "loop the loop" curve |
| Cartesian parametrization: The kinematic equation of motion is given by: Curvilinear abscissa and radius of curvature: 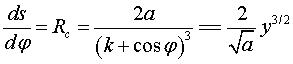 . . |
 |
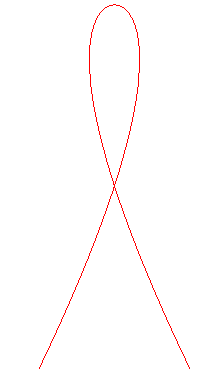
For k = 1 (case of the L'Hospital quintic) : Cartesian parametrization: Cartesian equation: Polynomial quintic. Vertex (0, a/4); isolated point double point Curvilinear abscissa: Radius of curvature: Parametrization of the evolute: |
A curve with constant reaction is a curve such
that if a particle descends along it by the pull of gravity (the gravitational
field is supposed to be uniform), then the reaction of the curve on the
particle has a constant intensity; conversely, the force applied by the
particle on the curve has a constant intensity.
 |
With Oy as the descending vertical, Newton's law,
projected on the normal, can be written: Solving it (use |
 |
In the case where k > 1, the curve is transcendental, ( |
|
|
In the case where k = 1, the curve is algebraic. |
 |
In the case where k < 1, the curve is transcendental again ( |
The evolute of such a curve is the solution of the following
problem (also posed by Jean Bernoulli): determining a curve on which to
wind the wire of a pendulum so that the tension of the wire of this pendulum
remains constant.
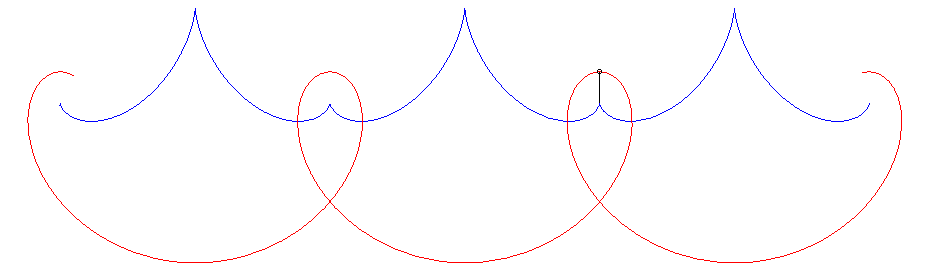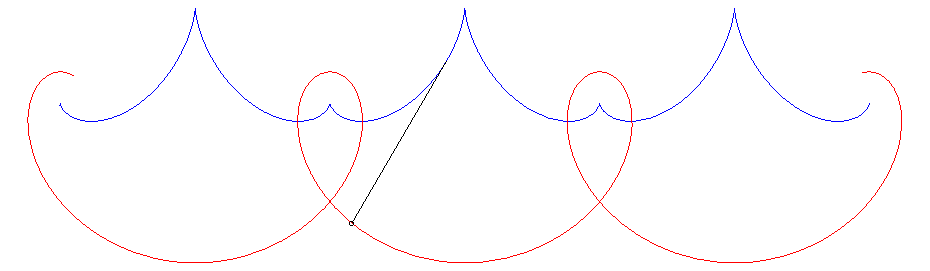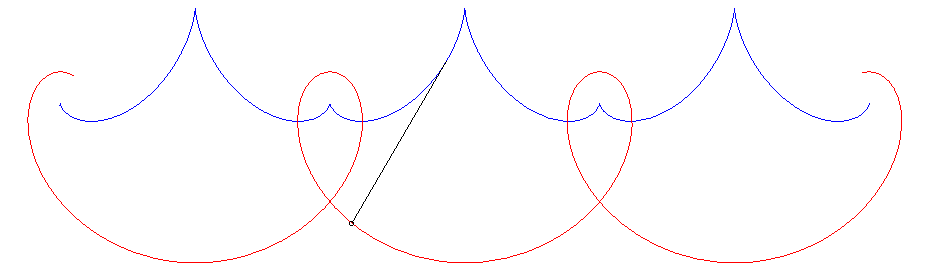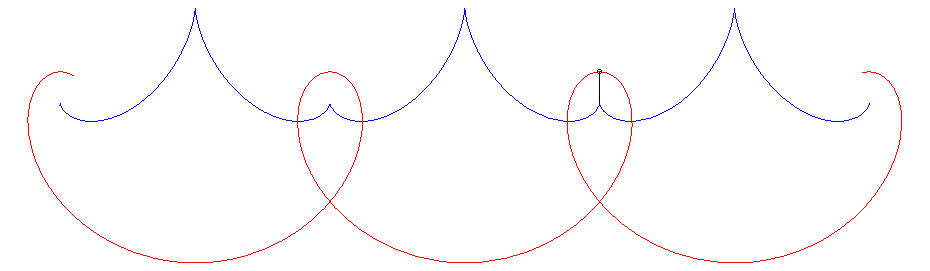
|
For other curves of motion of a massive point in a gravitational field under certain conditions, see isochronous, brachistochrone and tautochronous.

Is this double loop-the-loop in Adventureland a curve with constant reaction?
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017