Courbe de Polya

COURBE DE POLYA
Polya's curve, Polyasche Kurve

Courbe étudiée par Polya en 1913 [Über eine Peanosche Kurve, Bull. Acad. Sci. Cracovie, pp. 305-313, 1913].
Georges Polya (1887 - 1985) : mathématicien hongro-américain.
Liens :
Article de J.P. Kahane : www.univ-irem.fr/reperes/articles/29_article_192.pdf , voir aussi Quadrature n°15, 1993, p 39-46.
demonstrations.wolfram.com/PolyasSpaceFillingCurve/

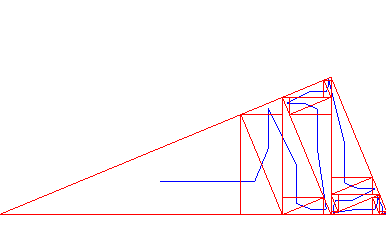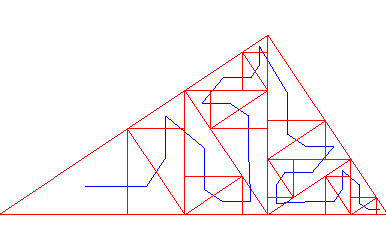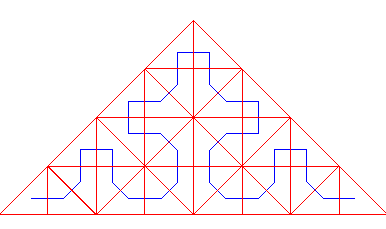
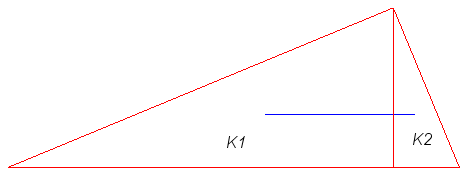
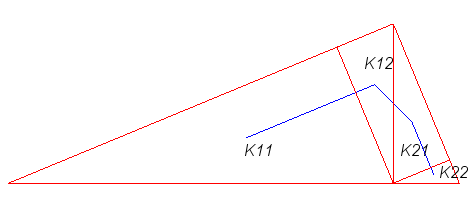
La courbe de Polya (version 1) est la courbe remplissant un triangle rectangle utilisant le partage du triangle en deux triangles semblables (voir la méthode générale sur la page des courbes remplissantes).

La courbe obtenue pour un triangle non isocèle est nettement moins esthétique que dans le cas isocèle...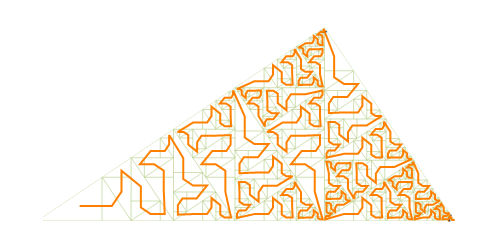

... mais l'esthétisme n'était pas le but recherché par Polya ; il cherchait un exemple de courbe de type Peano qui ne possède pas de point quadruple, contrairement à la courbe de Peano classique. Or justement, dans le cas isocèle, la courbe possède des points quadruples. D'ailleurs dans ce cas, la courbe n'est autre que la courbe de Césaro, ou un quart de la courbe de Sierpinski.

D'autre part, Benoit Mandelbrot, dans son livre : The fractal geometry of nature, page 64, mentionne une autre courbe remplissant un triangle isocèle rectangle, qu'il dénomme Polya's triangle sweep :

BALAYAGE TRIANGULAIRE DE POLYA

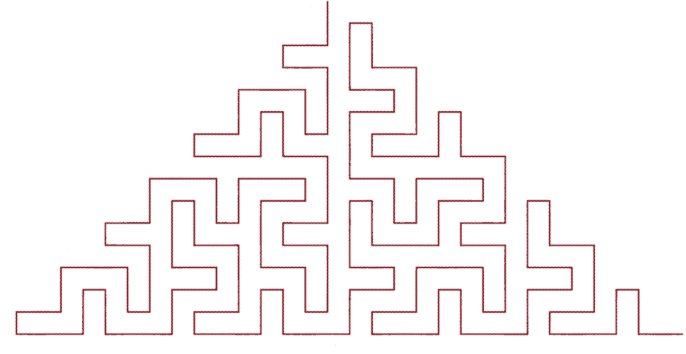
Lien :
www.fractalcurves.com/Root2.html

Code maple de tracé :
polya:=proc(A,B,n,e)
local C;
if n=0 then [A,B] else C:=(A+B)/2+e*I*(B-A)/2:
polya(C,A, n-1,-e),
polya(C,B,n-1,-e)fi end:
n:=7:display(seq(complexplot(polya(0,1,n,1)[k]),k=1..2^n),axes=none,scaling=constrained);

Étant donné un triangle ABC, isocèle rectangle en C, la "courbe" de Polya (version 2) est l'attracteur dans le plan des deux similitudes indirectes transformant, l'une (A, B) en (C, A), l'autre (A, B) en (C, B) ; ces deux similitudes étant de rapport , la dimension fractale de la courbe de Polya, qui est compacte et connexe, est ; ce qui est normal, puisque l'attracteur n'est autre que le triangle plein ABC, réuni avec son symétrique par rapport à (AC). Cette courbe est donc une courbe remplissante du triangle rectangle isocèle.

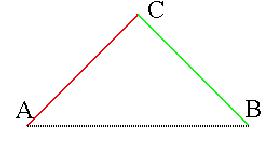
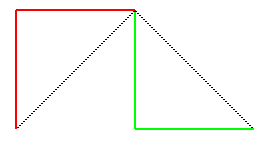
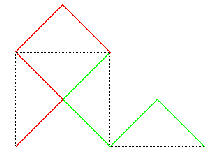
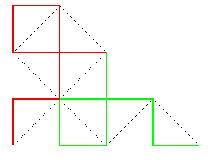
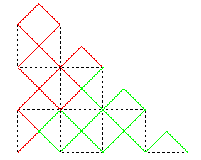
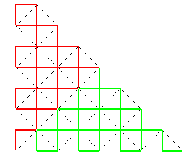
En partant de [AB], voici la suite des compacts convergeant vers cette courbe :

L'attracteur avec ses deux similitudes internes : Pas très fractal !

Comme pour la courbe du dragon, il y a une définition par pliage, mais ici, on plie la feuille alternativement dans un sens et dans l'autre.
Après déploiement et arrondissement des angles, cela donne :

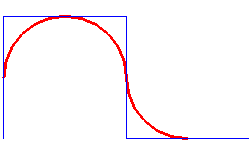
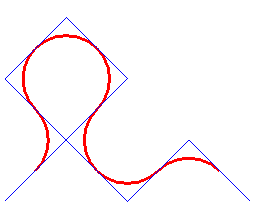
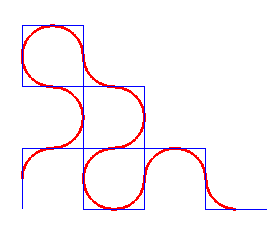
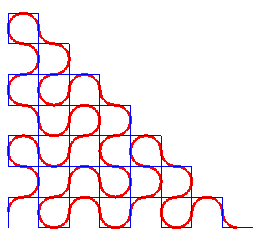
La suite S_ndes sens gauche (G) ou droite (D) des plis à l'étape n :

S₁ = D
S₂ = DDG
S₃ = GDDDGGD

possède alors pour définitions :

DEF 1 : où la notation S' signifie que le mot est écrit à l'envers et la notation S" signifie qu'on intervertit les D et les G.

DEF 2 : s'obtient à partir de en intercalant alternativement des D et des G, en commençant alternativement par un D ou un G ; par exemple :

Et comme pour la courbe du dragon, il y a une définition par rotations d'angle droit successives, l'angle changeant ici de signe à chaque étape ; on remarquera cependant qu'une courbe sur deux est image miroir de la courbe obtenue ci-dessus :

Pendentif polya en vente ici.

fractal suivant fractal précédent courbes 2D courbes 3D surfaces fractals polyèdres