Courbe du dragon

COURBE DU DRAGON
Dragon curve, Drachenkurve

Courbe étudiée par Heighway, banks et Harter en 1960.
Voir la programmation Povray sur cette page d'Alain Esculier.

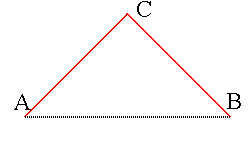
Étant donné un triangle ABC, isocèle rectangle en C, la courbe du dragon est l'attracteur dans le plan des deux similitudes directes transformant, l'une (A,B) en (A,C), l'autre (A,B) en (B,C) ; ces deux similitudes étant de rapport , la dimension fractale du dragon, qui est compact et connexe, est .

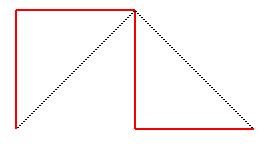
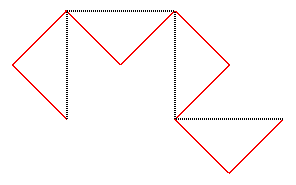
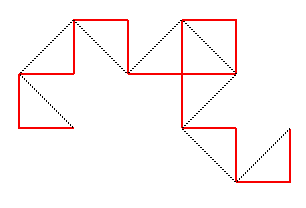
En partant de [AB], voici la suite des compacts convergeant vers cette courbe, constituant les courbes du dragon approchées ; ces courbes possèdent la propriété remarquable d'être continues et de ne jamais se traverser elles-mêmes, contrairement à celles de la courbe du C :

1
2
3

4
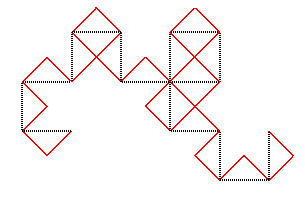
5
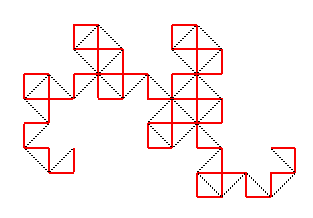
6

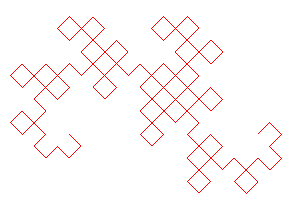
7
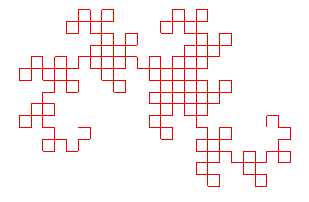
8
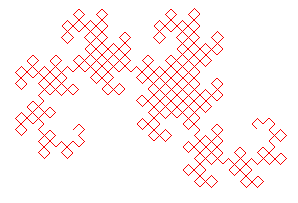
9

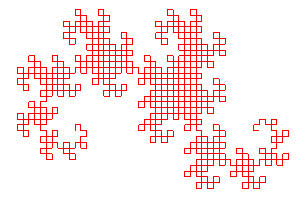
10
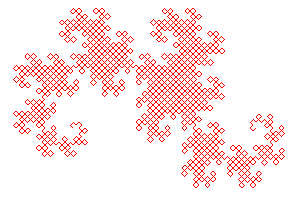
11 étape 9
12

Vue illustrant les deux similitudes internes

Si l'on prend, dans le plan complexe, A = 0 et B = 1, les deux similitudes sont et où ; et si l'on unit le dragon D avec son symétrique 1 – D par rapport au milieu de [AB] on obtient le dragon symétrisé D' :

On peut montrer que 2rD' n'est autre que l'ensemble unité U_rdes complexes qui s'écrivent comme sommes (finies ou infinies) de puissances à exposants entiers naturels du nombre r ; U_rest également l'attracteur des deux similitudes

Le dragon et le dragon symétrisé sont réunion quasi-disjointe de deux copies d'eux-même ; il y a exactement six figures du plan ayant cette propriété.

La courbe du dragon possède la propriété remarquable de pouvoir paver le plan :

Elle possède aussi une définition physique très simple ; si l'on plie une feuille de papier n fois sur elle-même, toujours dans le même sens, et que l'on déplie la feuille en remplaçant les plis par des angles droits, le profil de la feuille donne la courbe du dragon à l'étape n.

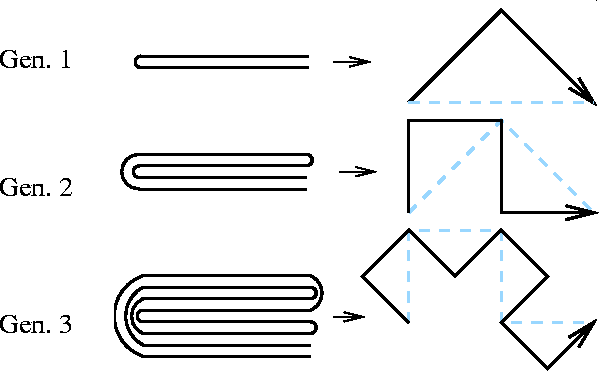
On peut en déduire une construction géométrique simple de la courbe approchée du dragon d'ordre n : la ligne orientée D_n s'obtient à partir de D_n-1 en prolongeant cette dernière à partir de son extrémité par une rotation autour de cette extrémité de +90° de la figure D_n-1.

La suite S_ndes sens gauche (G) ou droite (D) des plis à l'étape n :

S₁ = D
S₂ = DDG
S₃ = DDGDDGG

possède de nombreuses définitions remarquables :

DEF 1 : où la notation signifie que le mot est écrit à l'envers et en intervertissant les lettres D et G.

DEF 2 : s'obtient à partir de en intercalant alternativement des D et des G, en commençant par un D ; par exemple :

DEF 3 : prendre le système de Lindenmayer sur l'alphabet ABCD avec la transformation

en partant de A, puis remplacer A et B par D, et B et C par G.

Les sont les préfixes d'une suite infinie S = (u_n) , appelée suite du dragon.

DEF 4 : où f(D) = G et f(G) = D.

DEF 5 : u_n = D si le 1 le plus à droite de la décomposition en base 2 de n est précédé d'un 0, u_n = G sinon.
Par exemple : .

Voir aussi le balayage triangulaire de Polya, qui constitue une variante de la courbe du dragon.

Pour des informations sur la frontière de la courbe du dragon, voir www.poignance.com/math/fractals/dragon/bound.html.

fractal suivant fractal précédent courbes 2D courbes 3D surfaces fractals polyèdres