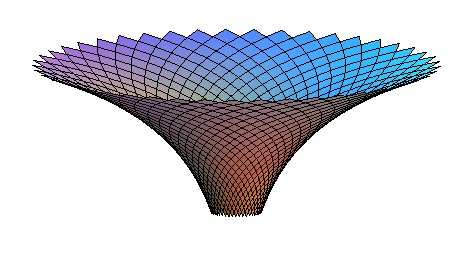
Cylindrical equation:  (case of the tower) or , i.e.  (case of the funnel). Cartesian parametrization:  (case of the tower).Première forme quadratique fondamentale : . First fundamental quadratic form:  . Second fundamental quadratic form:  . In the case k = 1, cartesian parametrization the coordinate lines of which are the asymptotic lines:  (view opposite).

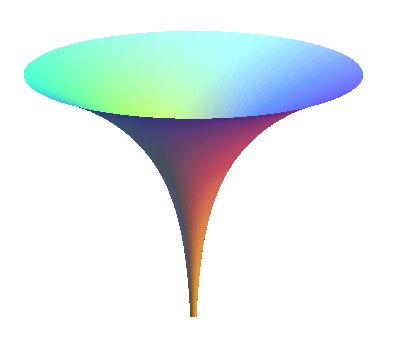
The tower with constant pressure is the surface of revolution obtained by rotating a logarithmic curve around its asymptote.
Its name comes from the fact that, if this surface is filled with a homogeneous material, then the pressure applied on any horizontal section by the upper part is constant.
 

Derivation of the equation: The pressure at the altitude z is equal to ; assuming P constant and differentiating, we get the differential equation: which immediately gives the result, with . Remark: if we take the variation of g due to the altitude into account, , we get the surface , with , represented opposite. Much as the first one has a straight line as asymptote, this one has an asymptote cylinder. Note that this tower, extended to infinity, would have an infinite mass, but finite weight...

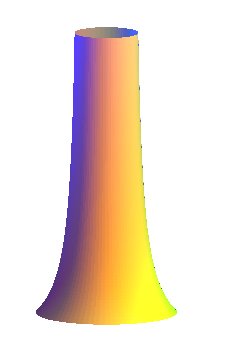See also Gabriel's horn.
 
 

next surface

previous surface

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL  2017