Zoom on the loop.

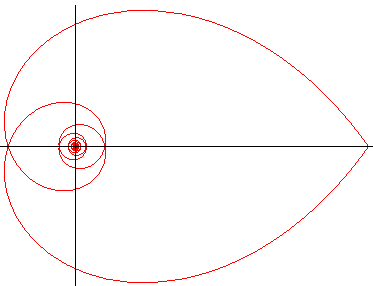Polar equation: . Curvilinear abscissa: . Curvature radius: .

A branch of the curve can be used to travel along a semicircle.

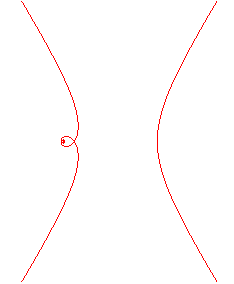
Catalan's curve is the solution of the following problem: finding the curve that, when rolling without slipping on a line D, has a point in its plane describing a circle tangent to D. To put it simply, Catalan's curve is the solution of the problem of the circular roulette.

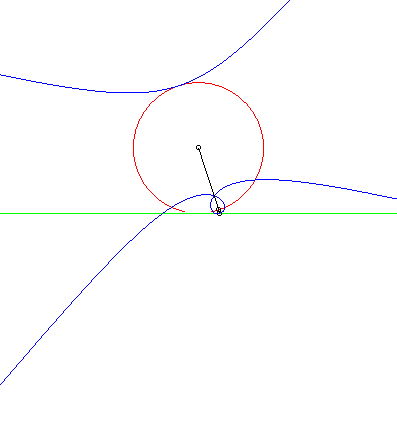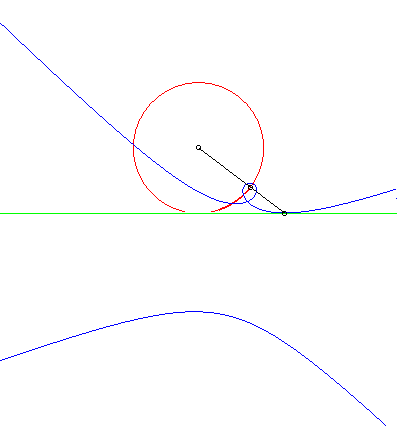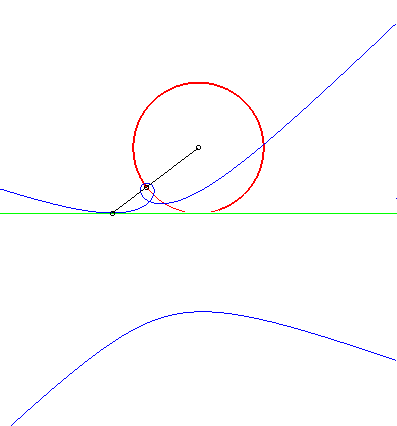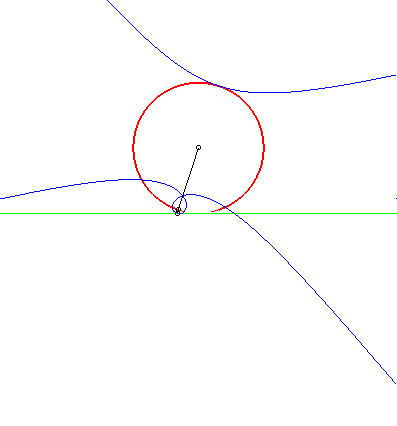As a consequence of the theorem stating that glissettes of a curve, with a linear base, are the roulettes of the evolute of the curve, with a linear base, Catalan's curve is the evolute of the tractrix spiral (which is the solution of the problem of the circular glissette).

Calculating the curvilinear abscissa shows that Catalan's curve is a solution of the equation , whose other solution is the circle.

Writing the polar equation as  shows that it is the polar medial curve of two hyperbolic spirals.

If we want a point of the plane of the rolling curve to describe a circle that is not tangent to the base, we get a rolling curve with polar equation  where a is the radius of the circle and d the distance of the centre of the circle to the base.
It is a polygasteroid, evolute of the tractory of a circle.
 
 

next curve

previous curve

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL  2017