Lintearia

LINTEARIA

Problem posed and solved by Jacques Bernoulli in 1692. He named the curve lintearia after the Latin word linteum meaning linen cloth.
Other named proposed: tarpaulin, by analogy with the catenary.

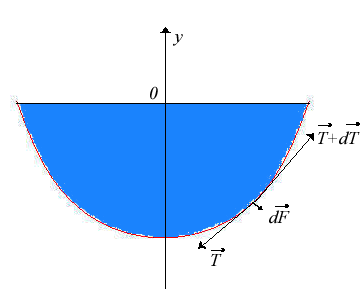
The lintearia is the shape taken by the profile of a rectangular tarpaulin attached to two horizontal bars, full of water up to the two bars (two planes limit the flow of water), and placed in a uniform gravitational field. The tarpaulin is supposed to be flexible, infinitely thin, inextensible, and without proper mass.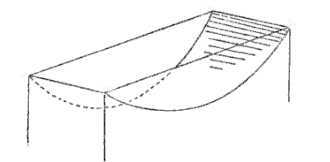

With the notations of the above figure (

= transversal tension of the tarpaulin at M), we write that the sum of the forces at M is zero:

where

, which means that the pressure force is proportional to the depth y and to the infinitesimal length ds, and that it is perpendicular to the profile of the tarpaulin.

This can be simplified to , and, by integrating, we get .

Therefore 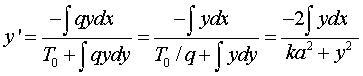, and, by eliminating the integral, we get the differential equation of the lintearia: .
With , we get the parametrization: , for , which is none other than the elastic curve (swap x and y).

Therefore, the lintearia is also the curve for which the curvature is proportional to the depth, result that could have been directly obtained by virtue of the Laplace law.

For 0 < k < 1, the lintearia is open, for k1 = -0.65222..... < k < 0, it is closed; the value of k1 is the limit value corresponding to the physical problem.

Remark: for a pressure force still proportional to y but also to the infinitesimal length dx instead of ds, oriented towards the bottom, i.e. , we would get a sinusoid.

See the dangling drop, generalisation to 3D-space of the lintearia.

Compare with the skipping rope curve.