Curve

CURVE

It is a very good question and I do not thank you for asking it to me!

Indeed, defining a curve in a general way is impossible:

If we say that a curve is a part of the plane homeomorphic to a line, then is not a curve.

If we say that a curve is a part of the plane for which any point has a neighbourhood homeomorphic to a line or a half-line, in other words, a topological manifold of dimension 1, then is not a curve.

If we call topological curve this latter notion, then any connected component of a topological curve is a topological curve, and there are, up to homeomorphism, only 3 connected topological curves: the circle S¹, the line R and the half-line R₊. In the first case, the topological curve is called "closed", or "Jordan curve", in the second case "open", and in the third "semi-open".

If we say that a curve is a part of the plane for which any point has a neighbourhood composed of the reunion of a finite number of parts homeomorphic to the line, then is not a curve.
If we say that a curve is a part of the plane for which any point has a neighbourhood composed of the reunion of a countable family of parts homeomorphic to the line, then is not a curve (it is a rose, dense subset of the disk, with n irrational).

If we say that a curve is a part of the plane, image of an interval of R by a continuous function (in other words, the support of a continuous parametric curve), then the hyperbola 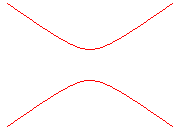is not a curve, but is a curve and, more generally, all the compact connected and locally connected parts, which are exactly the images of [0,1] by the continuous functions, are curves.

If we say that a curve is a part of R² with equation f(x, y)= 0 where f is continuous, or even indefinitely differentiable, then a strip of non-zero width is a curve.

If we say that a curve is a part of R² with equation f(x, y)= 0 where f is differentiable and its differential is never zero, then we only get simple curves (i.e. without double points)...

See generic curve for a more general notion than that of simple closed topological curve.

next curve previous curve 2D curves 3D curves surfaces fractals polyhedra