and 
are
called mating profiles associated to the centres of rotation O1
and O2 (the gear hubs) if
can turn around O1 and
around O2 so that the two curves
always are in contact (i.e. tangent without slipping on one another).
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
MATING GEAR PROFILES
| Notion studied by Euler and by Miquel
in 1838.
Other name, given by Miquel: syntrepent curves, literally "that turn together". |
Two curves
and are
called mating profiles associated to the centres of rotation O1
and O2 (the gear hubs) if
can turn around O1 and
around O2 so that the two curves
always are in contact (i.e. tangent without slipping on one another).
The get the curve
when the curve ,
the hub O1 and the distance d
= O1O2
are given, one only has to determine the movement
of a plane over a fixed plane the base of which is
and a roulette of which is the circle with centre O1
and radius d: the rolling curve is then the curve .
Writing 
the polar coordinates of the current point on
in a frame centred on O1, and, similarly, 
for in
a frame centred on O2, the relation
between
and is
given by:
 and 
are nonnegative. If we accept negative values, the second case is equivalent
to the first one by changing
into its opposite. |
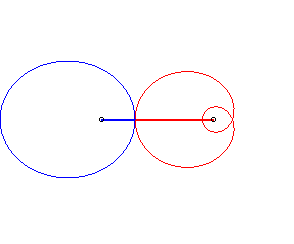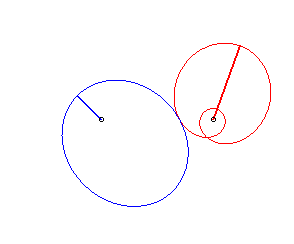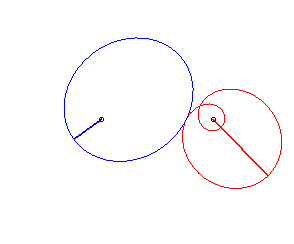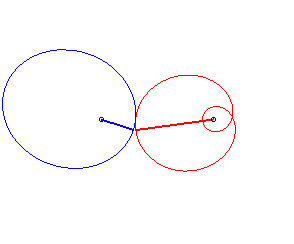
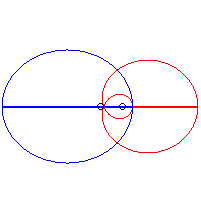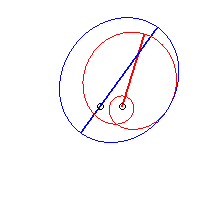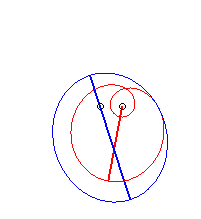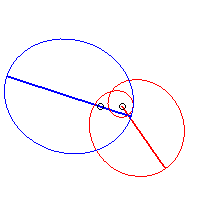
Remark: By the Descartes theorem, the contact point between the two mating profiles is always aligned with the two hubs.
Examples:
- if
is a circle with radius a and the hub is at its centre,
is a circle with radius |d - a|.
- if
is linear, located at distance a from O, then the equation
of is 
,
which gives:
if d > a: 
with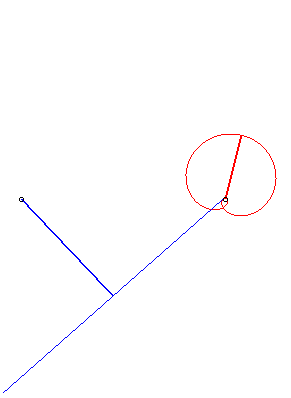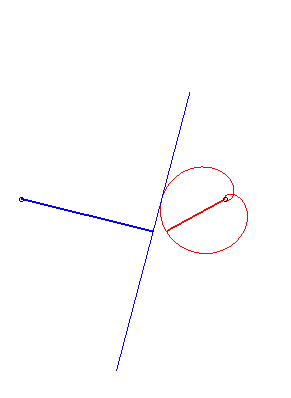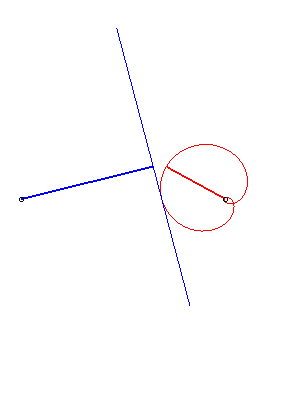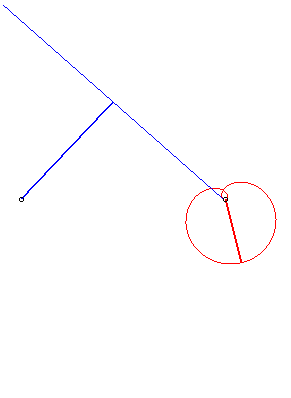 
 |
if d = a:  |
if d < a: 
with 
(polygasteroid with
e
> 1)
|
is an ellipse, with polar equation 
(the hub is therefore a focus),
is a polygasteroid,
with polar equation 
,
where 
(n represents the number of turns completed by
when completes
one turn); if 
is the semi-major axis of the ellipse, the distances to the hubs are given
by 
for
gears turning in opposite directions, and 
for gears turning in the same direction.
Case n = 1 (i.e. k = 2):
is an ellipse isometric to .
The ellipse is said to be isotrépente for its focus.
 |
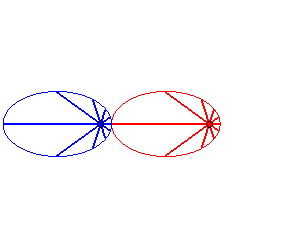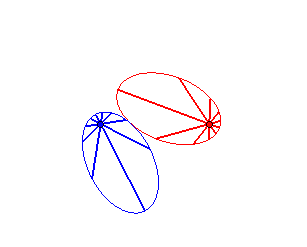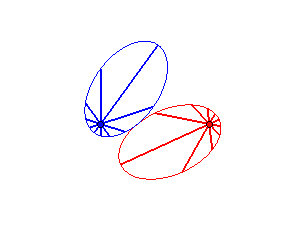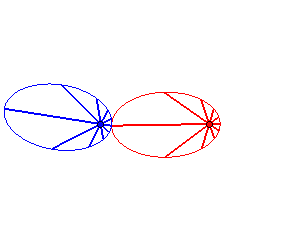Case n = 2: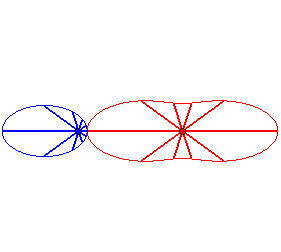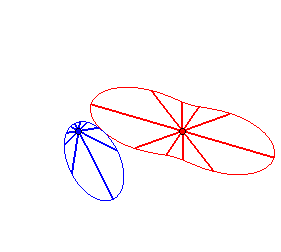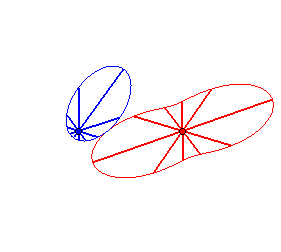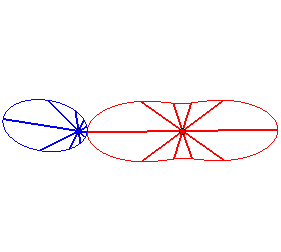
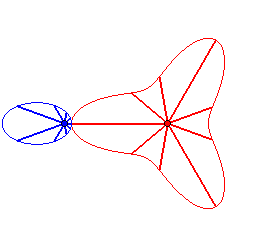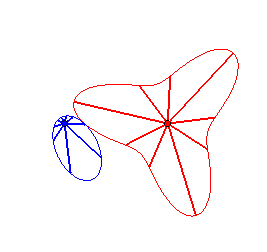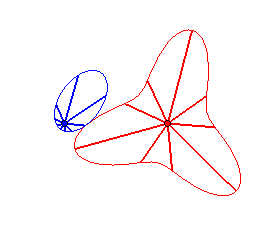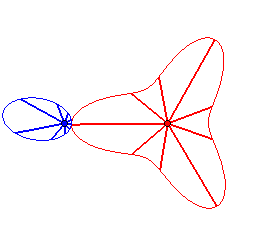
is an inverse of the peanut.
   )
the ellipse is included inside its mating profile. |
 |
  |
Remark: if
is a hyperbola, the same property holds, but is not illustrated here, because
the hyperbola is not a closed curve. See the case n = 1 on the page
of the hyperbola.
| - if
is a logarithmic spiral,
is an isometric logarithmic spiral; the logarithmic spiral is therefore
also an isotrépente curve.
This mechanism was discovered by the astronomer Ole Rømer. It is used in the "varistart" system, and allows for a progressive increase of the rotation speed of a gear.  |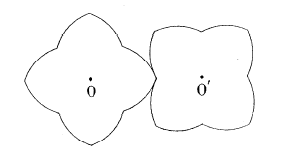
 |
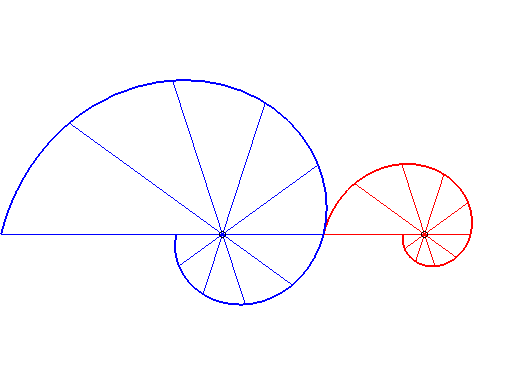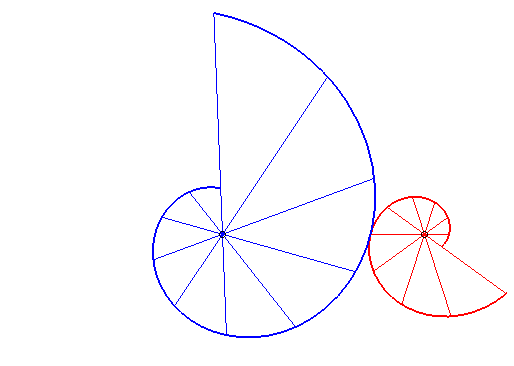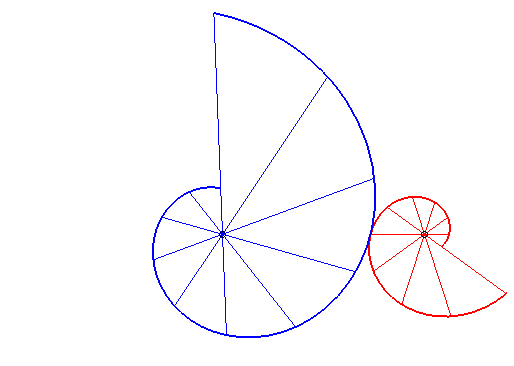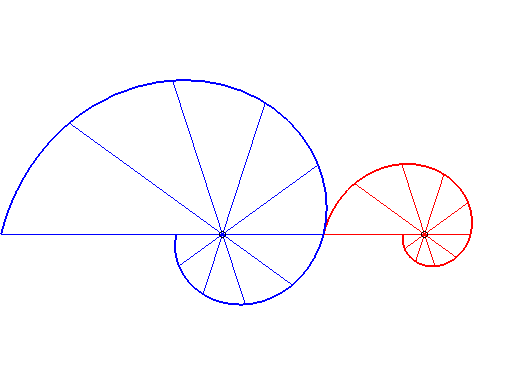- if
is a cardioid:
(hub at the cuspidal point),
the parametrization of
is: 
(d = ka). Opposite, the case k = 18/5. |
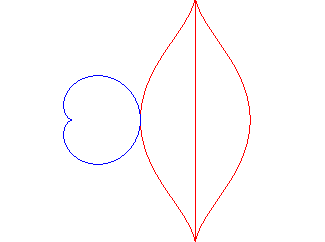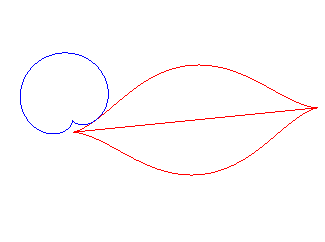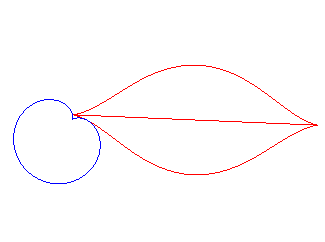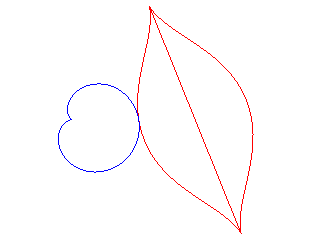
The mouth with the heart... |
if
is a circle: 
(hub on the circle),
the parametrization of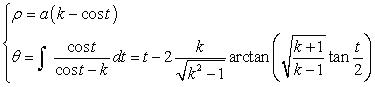
is: 
(d = ka). Opposite, the case k = –5/3. |
 |
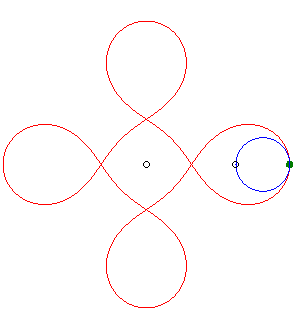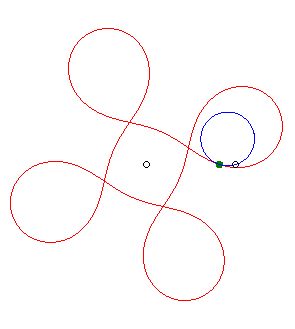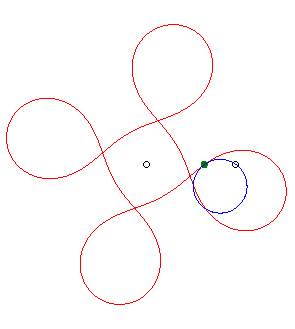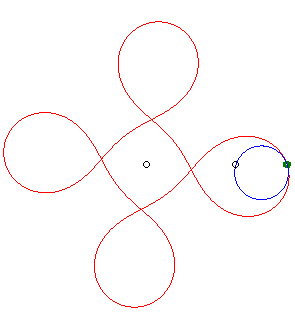| Schroeder
gears dating from 1867, coming from the Musée des Arts et Métiers.
The bottom curve
is a limaçon of Pascal.
See also this link. |
  |
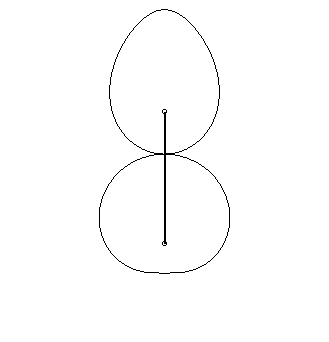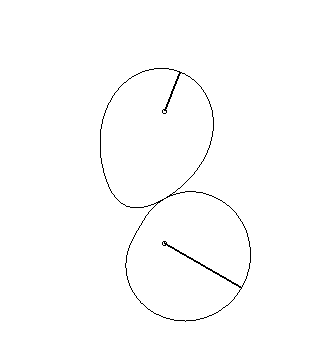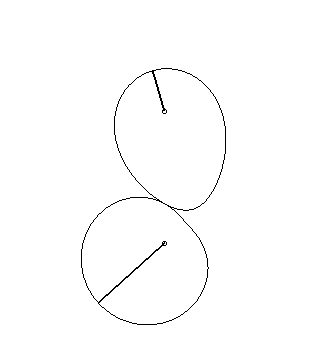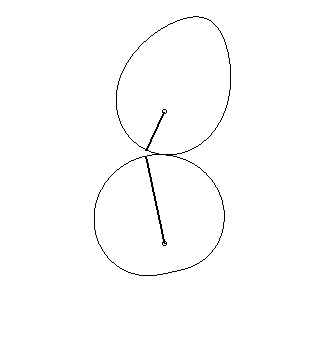When the hub of one of the gears is at infinity, we get
a wheel-road couple.
| We saw above that if we attach one of the gears and that
we make the other one roll on it, the latter's hub describes a circle.
This enables to imagine "Shaddock" vehicles like the one represented opposite...
(by Alain Esculier: see at the bottom of this
page)
For similar vehicles, but with a linear motion, see the next page. |
 |
See also the hyperboloid gears, generalisation to space
of this planar notion, at the bottom of this
page.
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL , Jean LEFORT, Alain ESCULIER 2017
,
the polar equation of 
where
g
is defined by:
.
.
,
the polar equation of 
.
where g is
defined by:
.
.
.