COURBE DE BÉZIER RATIONNELLE
Rational
bezier curve
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
COURBE DE BÉZIER RATIONNELLE
Rational
bezier curve

| Paramétrisation affine : Courbe algébrique rationnelle de degré £ n. |
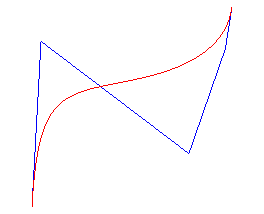
Une suite de points pondérés - les
points de contrôle -
étant donnée, la courbe de Bézier rationnelle associée
est la courbe de paramétrisation ci-dessus ; la courbe passe par
A0
(pour t = 0) et An (pour
t
= 1), et la portion qui joint ces points est tracée dans l'enveloppe
convexe des points de contrôle ; la tangente en A0
est
(A0A1)
et celle en An (An-1An).
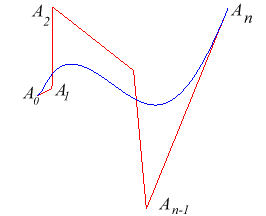
Lorsque les masses ak
sont égales, on retrouve les
courbes
de Bézier polynomiales.
Cette courbe est la projection conique (transformation )
de la courbe de Bézier 3D polynomiale dont les points de contrôle
sont les points Ãk définis
par
.
Les courbes de Bézier rationnelles recouvrent
donc toutes les courbes rationnelles.
La seule conique polynomiale étant la parabole, les courbes de Bézier simples ne permettent pas de représenter exactement un cercle, mais c'est possible avec les courbes de Bézier rationnelles.
Par exemple, si l'on prend un polygone de contrôle formé de deux segments égaux orthogonaux, la courbe de Bézier simple est une parabole ; si l'on double l'une des masses à une extrémité, on obtient un cercle :
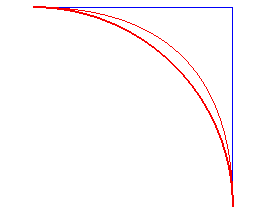
En gras la courbe de Bézier rationnelle, qui est un cercle.
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL,
Jacques MANDONNET 2000