Courbe du diable

COURBE DU DIABLE
Devil's curve, Teufelskurve

Courbe étudiée par Cramer en 1750 et Lacroix en 1857.
Le nom de cette courbe viendrait de ce qu'elle représente la section d'un diabolo (= diable étymologiquement), ou bien de ce que son tracé était considéré comme difficile à obtenir comparé à la simplicité de son équation cartésienne.
Autre nom : courbe de Cramer.

Équation polaire :

.
Équation cartésienne :

, soit

.
Quartique de genre 2.

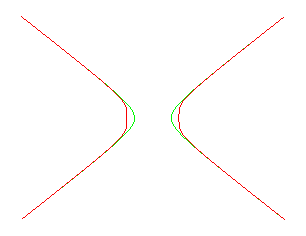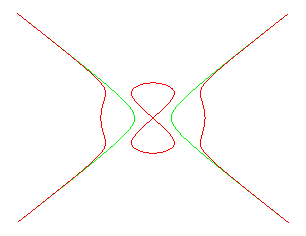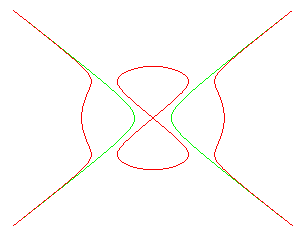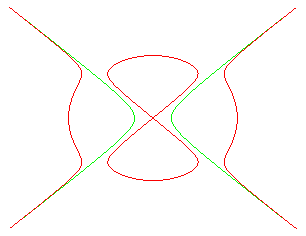
La courbe du diable est la courbe donnée par les équations ci-dessus.

Elle est formée de deux branches allant à l'infini et d'un huit qui n'apparaît que lorsque b > a.

Les deux branches infinies peuvent se construire géométriquement à partir de l'hyperbole équilatère : (en vert sur la figure) comme suit : un point H décrivant l'hyperbole, construire un triangle rectangle en H OHN avec HN = b ; ces deux branches sont les lieux des points M de (OH) tels que OM = ON.

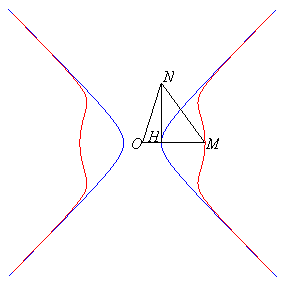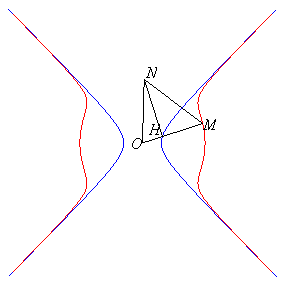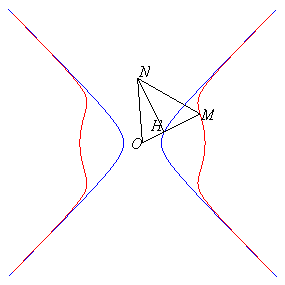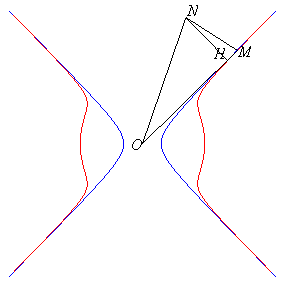angle droit en H, HN = cte = b, OM = ON.

Le huit central se construit géométriquement à partir de la même hyperbole équilatère comme le lieu d'un point M d'un triangle rectangle en O OHM d'hypoténuse de longueur constante (= b), le point H décrivant l'hyperbole.

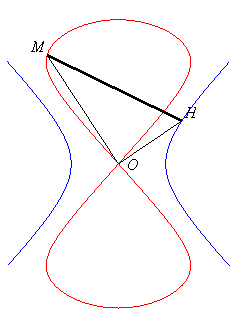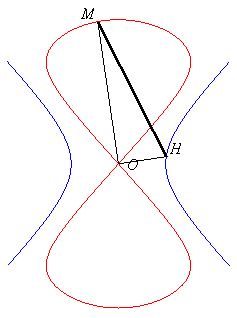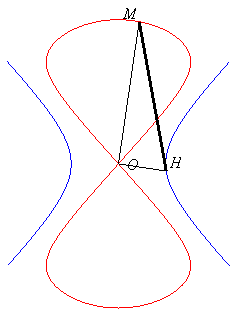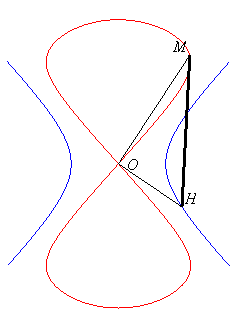angle droit en O, HM = cte = b. Une construction équivalente consiste à dire que le huit de la courbe du diable est le lieu du centre des cercles de rayon constant ( = b) passant par les extrémités des diamètres (i.e. deux points symétriques par rapport à O) d'une hyperbole équilatère.

Pour b = 0, on obtient bien sûr comme cas limite l'hyperbole.

L'intérêt de la courbe du diable semble être principalement d'être la plus simple des courbes de genre 2.

Voici comment Cramer décrit délicieusement cette courbe :
"On aura la courbe entière formée d'un huit-de-chiffre qui se noue à l'origine, & deux autres parties séparées qui, après avoir serpenté à droite et à gauche, mais à quelque distance du huit-de-chiffre, jettent quatre branches à l'infini, une dans chacun des 4 angles des coordonnées."

courbe suivante courbe précédente courbes 2D courbes 3D surfaces fractals polyèdres