Courbe étudiée et ainsi nommée par C. Masurel en 2013.

 

Équation polaire :  ( n > 0) soit . Paramétrisation polaire, pour  : . Angle tangentiel polaire : . Abscisse curviligne :  pour , pour n = 1 (provenant de ).

La tangente bleue au point d'intersection avec le cercle d'inversion est la droite  . Ici, tracé pour n = 2.

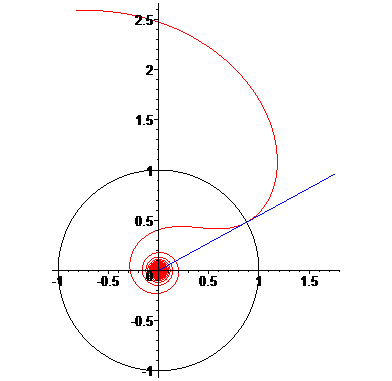
Les spirales anallagmatiques sont les courbes d'équation polaire donnée ci-dessus.
Comme leur nom l'indique, et comme leur équation le montre, elles sont invariantes par inversion (de pôle O et de puissance a).
 

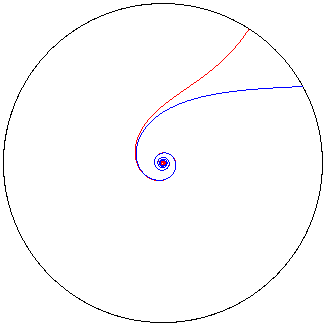
La branche extérieure au cercle d'inversion est asymptote à la spirale archimédienne d'indice 1/n :

et la branche intérieure est asymptote à la spirale archimédienne d'indice –1/n :

 

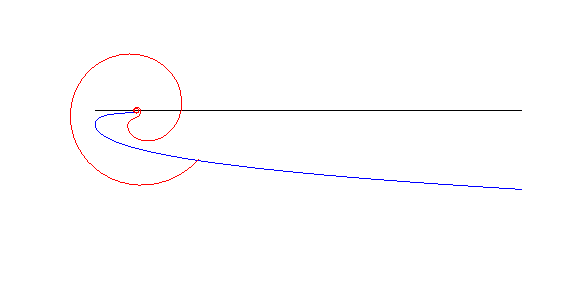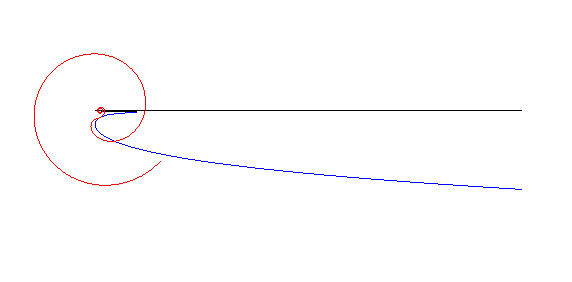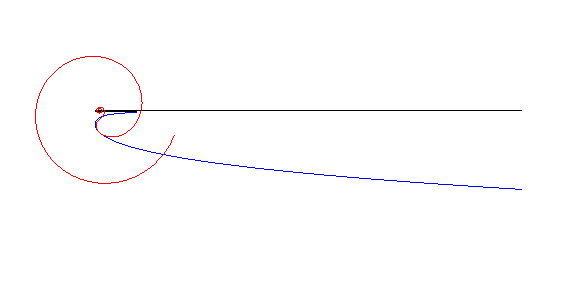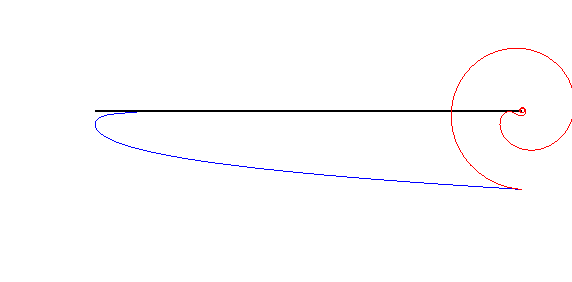
Les spirales anallagmatiques sont les "roues" associées aux courbes de poursuite rectiligne (voir à couple roue/route). Plus précisément, si on fait rouler comme ci-contre la spirale anallagmatique de paramètre n sur la courbe de poursuite de paramètre n (= vitesse du maître/vitesse du chien), le pôle de la spirale décrit l'asymptote (cas n1) ou la tangente sommitale (cas n < 1) de la courbe de poursuite.

 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL  2013