COURBE DE WUNDERLICH
Wunderlich's curve, wunderlichsche Kurve

| fractal suivant | fractal précédent | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
COURBE DE WUNDERLICH
Wunderlich's curve, wunderlichsche Kurve

| Courbes étudiées par Wunderlich
en 1973.
Walter Wunderlich (1910 - 1998) : mathématicien autrichien. |
Les courbes de Wunderlich sont des variantes de la courbe
de Péano ternaire.
Pour la courbe de Péano
classique, on partage le carré en neuf, et on choisit un chemin
continu passant par les 9 carrés : 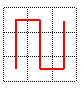 ; les 9 carrés étant ensuite chacun partagés en 9,
c'est le chemin image miroir
; les 9 carrés étant ensuite chacun partagés en 9,
c'est le chemin image miroir 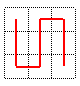 qui
est choisi dans un carré sur deux, en commençant par le deuxième. qui
est choisi dans un carré sur deux, en commençant par le deuxième. |
 |
 |
 |
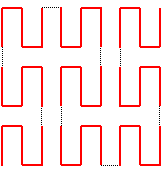
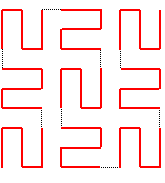
| Pour la courbe de Wunderlich, on choisit le même
ordre des 9 carrés, mais le chemin choisi dans chacun des 9 carrés
est obtenu par rotation du chemin de base.
On obtient ainsi une courbe où la proportion des segments verticaux est égale à celle des horizontaux, donc plus harmonieuse. Comme pour la courbe de Péano, la courbe de Wunderlich est l'attracteur d'une famille de 9 similitudes de rapport 1/3 ; les 9 similitudes sont directes, alors qu'il n'y en avait 5 directes et 4 indirectes pour Péano. |
 |
 |
 |
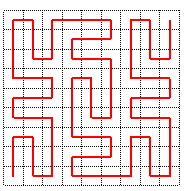
| Dans la version ci-contre, le chemin image miroir a été choisi dans tous les carrés ; la courbe est simplement symétrique de la précédente par rapport à la diagonale descendante. |  |
 |
 |
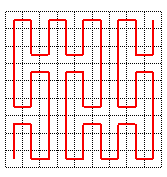
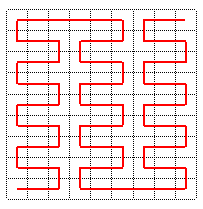
Ici, le chemin image miroir  a
été choisi dans un carré sur deux, en commençant
par le premier. a
été choisi dans un carré sur deux, en commençant
par le premier.
Il y a donc en fait 29 = 512 variantes possibles (voir sur aesculier.fr/fichiersMaple/peano/peano.html un programme de tracé de ces courbes) |
 |
 |
 |
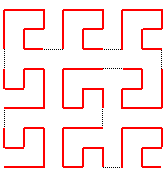
Dans cette dernière version de Wunderlich, le
chemin de départ choisi est différent : ; et c'est le même chemin qui est choisi, avec diverses orientations
ou symétries, dans chaque carré.
; et c'est le même chemin qui est choisi, avec diverses orientations
ou symétries, dans chaque carré.
Là aussi 512 variantes possibles (voir toujours aesculier.fr/fichiersMaple/peano/peano.html ) |
 |
 |
 |
| fractal suivant | fractal précédent | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL
2011