Sites : Un fan du pavage du Caire Wikipedia anglais Animation wolfram Animations de cette page réalisées par Alain Esculier.

 

Le pavage du Caire, ainsi nommé car on le trouve comme motif des trottoirs du Caire, est le pavage plan monoédrique obtenu en prenant pour pièce de base un pentagone convexe ABCC'B' ayant les caractéristiques suivantes : les côtés AB, BC,AB',B'C' sont égaux et les angles en B et B' sont droits. Sa forme est donc entièrement définie par l'angle en A,  compris entre 90° (cas du carré) et 180° (cas du rectangle 2/1). Les angles en C et C' sont égaux à .  L'angle BIB' où I est le milieu de [CC'] est droit. Si a = AB, . Remarquons que si tous les quadrilatères convexes pavent le plan, ce n'est pas le cas de tous les pentagones. On est donc en présence d'une famille de pentagones paveurs : voir cet article, et cette page.

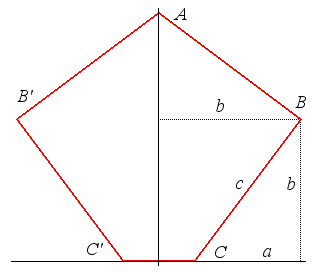
Un moyen de construire le pentagone du Caire est de partir d'un triangle rectangle de côtés a,b,c, a<b, c=rac(a²+b²), et de prendre A=(0,a+b), B=(b,b), C=(b–a,0) (vérifier que l'angle en B est bien droit). On obtient un pentagone de côtés 2(b–a) et c (4 fois). Si (a,b,c) est un triplet pythagoricien, le pentagone a ses côtés entiers (cf. cette suite de l'OEIS). Le triplet choisi ci-contre est le classique (3,4,5).

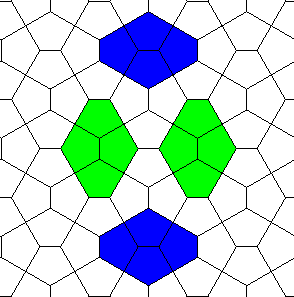
On obtient un pavage à deux types de sommets, ceux de degré 4 (4 angles droits), et ceux de degré 3 (2 angles , un angle ). Le pavage peut aussi être vu comme la superposition de deux pavages formés de grands hexagones issus de 4 pentagones (dénommés "hexagones du Caire"), les uns verticaux, les autres horizontaux, ce qui est la clé du côté esthétique de ce pavage.

Cas particuliers remarquables :
 

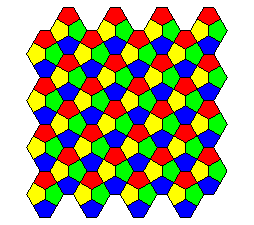
Pavage du Caire semi-régulier de deuxième espèce. , . Les sommets sont tous réguliers, soit de degré 3, soit de degré 4. Ce pavage est optimal parmi les pavages pentagonaux convexes en ce sens qu'il minimise le périmètre du pavé pour une aire donnée. Il n'est pas le seul, il y a aussi un pavage pentagonal prismatique (voir cet article).
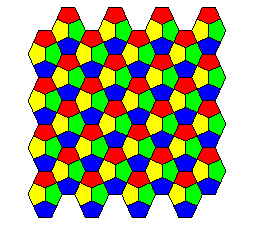
Pavage du Caire équilatéral (tous les côtés sont égaux) : , .
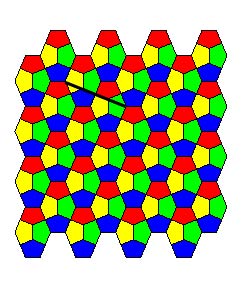
Pavage du Caire "cordouan" (voir explications sur cette page ), , Le trait noir indique des alignements qui ont lieu dans ce cas.

Vrai pavage des trottoirs du Caire ? Le trait noir sur la photo ci-contre indique des alignements, qui après calculs, conduisent aux valeurs :. De plus, ce cas se construit très simplement à partir d'un quadrillage, comme indiqué ci-contre, ce qui conduit à supposer que c'est bien le modèle qui a été utilisé.... Note : ce pavage est très proche du cas  qui pourrait être qualifié de "doré", puisqu'il fait intervenir le nombre d'or. La photo (Helen Donnelly) est tirée de ce site, qui recense aussi d'autres trottoirs du type cairote dans le monde, par exemple au Japon.

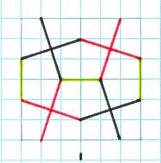
Construction du cas  .

 
 

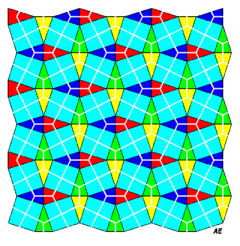
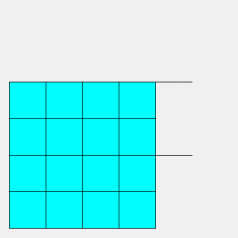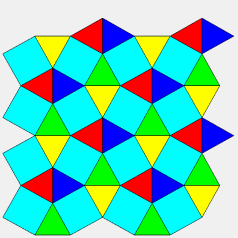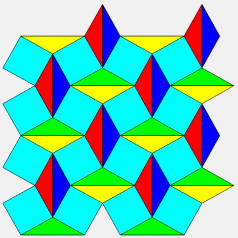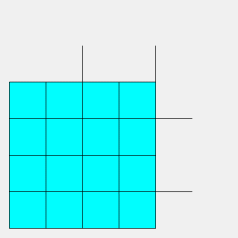
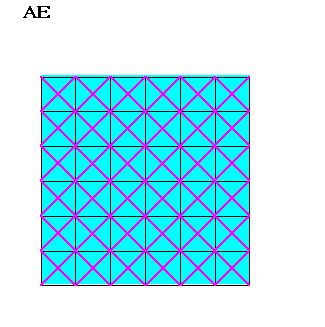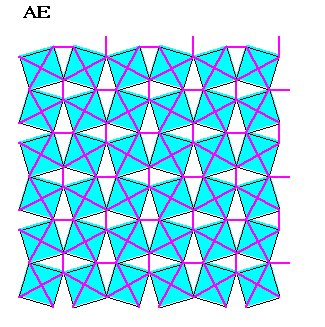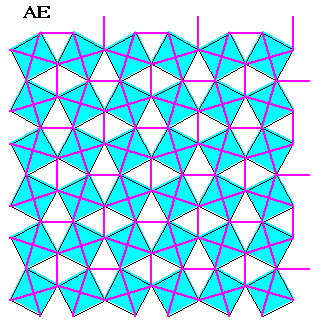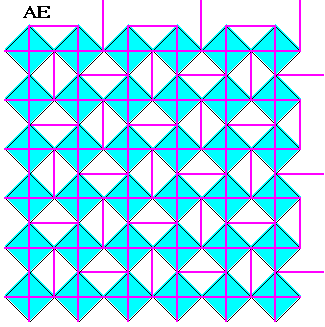
Le pavage dual obtenu en prenant comme sommets les milieux des segments AI est formé de carrés et de triangles, les triangles étant équilatéraux dans le cas semi-régulier. C'est le quadrillage adouci, obtenu en faisant pivoter les sommets des carrés les uns sur les autres. Ce qui est remarquable, c'est qu'on réobtient ce quadrillage adouci en traçant, dans le pavage du Caire (en rose ci-contre, avec clignotement bleu), uniquement les triangles ACC' (en blanc ci-contre).

 

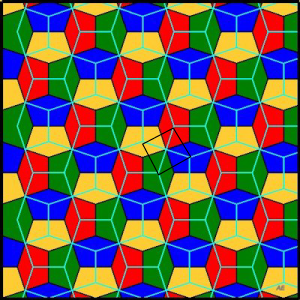
Inversement, si dans le tracé du dual du pavage du Caire, on remplace les bords des carrés par leurs diagonales, on réobtient un pavage du Caire.  Un calcul montre que ce dernier pavage est superposable au premier dans le cas du pavage cordouan défini ci-dessus. Les deux pavages sont alors issus l'un de l'autre par simple translation, comme on le voit ci-contre.

 

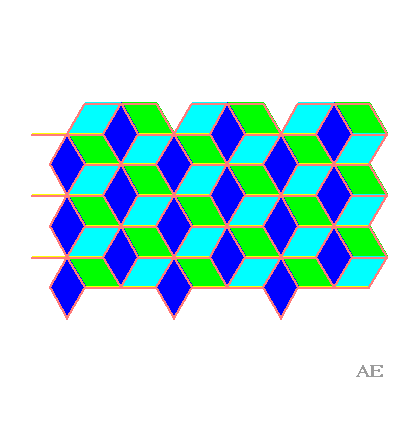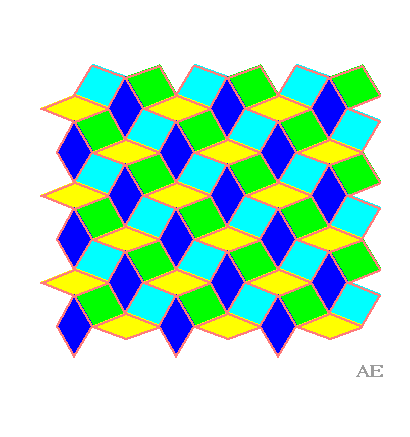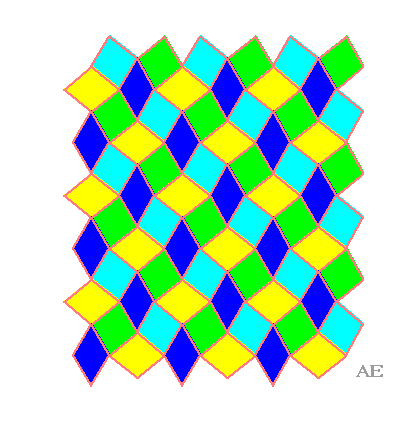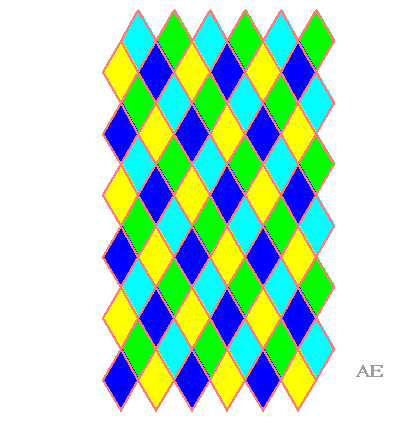
Cette animation part du quadrillage rhombique (3.6)2 par des losanges 60°/120° pour arriver au quadrillage régulier par des losanges. Lorsque les losanges verts et bleu ciel sont des carrés, on obtient le quadrillage adouci, à condition de séparer les losanges bleus et jaunes en deux triangles équilatéraux. Ce pavage est très apprécié des décorateurs, pour son effet de perspective de marches qui seraient justement... adoucies. Et comme on le voit ci-dessous, les Romains le connaissaient déjà (mosaïque exposée au Metropolitan, à New York).

 

Le maître du pavage, Escher, s'est intéressé au pavage du Caire, en entrelaçant les côtés, et en tentant, avec des fleurs, de faire croire que les pentagones sont réguliers ...

 

Les hexagones formés de 4 pentagones du Caire du cas semi-régulier peuvent être arrangés autour d'un hexagone régulier comme ci-contre pour former un pavage bi-pièces. À droite deux versions vérifiant les conditions du théorème des quatre couleurs (deux pavés limitrophes de couleurs distinctes). La deuxième coloration est "parfaite" en ce sens que chaque couleur est transformée en chaque autre par une isométrie laissant le pavage invariant.

Le motif de base.

 

Table à repasser Ikéa !

Chaise du Caire !

Jeu de miroir au pavillon ENEL (l'EDF italien) de l'EXPO de Milan 2015.

 

polyèdre suivant

polyèdre précédent

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL 2017