COURBE DE HILBERT

| fractal suivant | fractal précédent | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
COURBE DE HILBERT

| Courbe étudiée par Peano en 1890 et Hilbert
en 1891.
David Hilbert, 1862-1943 : mathématicien allemand. 
Voir aussi cet article. |
| Paramétrisation cartésienne définie
par récurrence par :
M(0) = (0, 0) et M(1) = (1, 0)
ces formules se traduisent par : |
Définition n°1 :
La courbe de Hilbert est l'unique courbe
de Peano binaire remplissant le carré [0, 1]2
et telle que M(0) = (0, 0) et M(1) = (1, 0).
Elle est donc définie par l'algorithme :
1) Partager [0, 1]2 en 4 "petits" carrés "égaux" ; numéroter chacun de ces carrés de sorte que deux carrés successifs se touchent par un côté, en commençant par le carré en bas à gauche, et terminant par le carré en bas à droite.
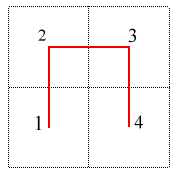
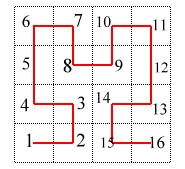
3) Recommencer ce processus à l'infini.
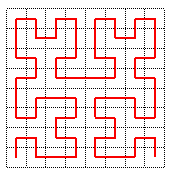


La courbe de Hilbert approchée du premier type d'ordre n est alors la ligne brisée joignant les centres successifs de ces carrés.

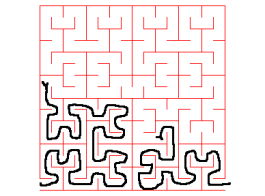
Le labyrinthe de Hilbert d'ordre n est la
réunion des côtés des carrés
excepté les côtés joignant deux carrés consécutifs
(et les deux entrées) :


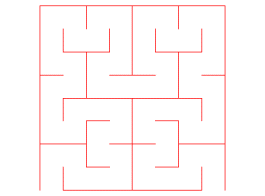

Les ,
pour t fixé, forment une suite de carrés (compacts)
emboîtés dont l’aire tend vers 0 ; leur intersection est donc
réduite à un point
, point courant de la courbe de Hilbert.
On démontre que la courbe est continue et que sa trajectoire est dense dans le carré de départ, donc égale à ce carré.
La courbe de Hilbert possède cependant des points multiples ; le point central par exemple est un point triple.
Voici quelques points remarquables avec leurs paramètres.
Définition n° 2 :
Etant donné un carré ABCD (ici A(0,0),
B(1,0),
C(1,1), D(0,1)), la courbe de Hilbert est la courbe limite associée
à la famille des 4 contractions suivantes
(avec pour segment de départ [AB]) :
- fA
: similitude indirecte de centre A, d'axe [AC] et de rapport 1/2
()
- fB :
similitude indirecte de centre B, d'axe [BD] et de rapport 1/2 ()
- fC :
homothétie de centre C de rapport 1/2 ()
- fD :
homothétie de centre D de rapport 1/2 ()
Dont le carré plein ABCD est l'attracteur.
La courbe de Hilbert approchée du deuxième
type d'ordre n est l'image itérée n-ième
de [AB] par f définie par.
 |
 |
 |
 |
 |
 |
Elle possède malheureusement des points doubles (que possède de toutes façons la courbe limite).
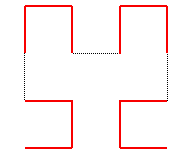
En prenant comme courbe de départ : ,
on peut retrouver la courbe de Hilbert du premier type, à condition
de raccorder les "U" entre eux :
,
on peut retrouver la courbe de Hilbert du premier type, à condition
de raccorder les "U" entre eux :
 |
 |
 |
 |
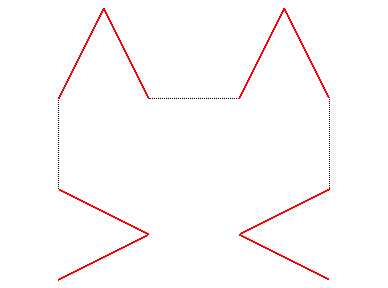
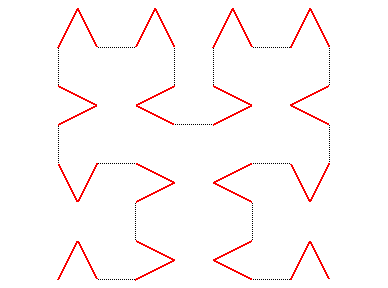
En prenant comme courbe de départ : 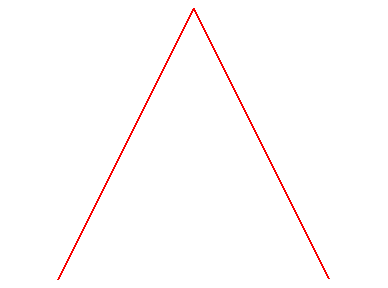 et
en raccordant, on obtient une suite de courbe convergeant aussi vers la
courbe de Hilbert :
et
en raccordant, on obtient une suite de courbe convergeant aussi vers la
courbe de Hilbert :
 |
 |
 |
 |


Monument en l'honneur de Péano situé à au lycée scientifique de Cunéo
| fractal suivant | fractal précédent | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2019