Courbe de Lebesgue

COURBE DE LEBESGUE
Lebesgue curve, Lebesguesche Kurve

Courbe étudiée par Lebesgue en 1904.
Henri Lebesgue (1875 - 1941) : mathématicien français.

La courbe est désignée en anglais par z-curve plutôt que Lebesgue curve (cf figure de droite).

Voir aussi cet article.

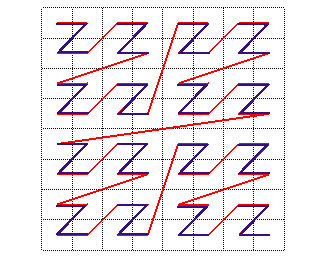Paramétrisation cartésienne : en posant

en base 3,

où f est la fonction de Cantor-Lebesgue ( si le développement ternaire impropre de t ne comporte que des 0 ou des 2 (c'est-à dire, si t appartient à l'ensemble de Cantor), f(t) est le nombre obtenu en changeant les chiffres 2 en des 1, nombre alors lu en base 2. Si le développement ternaire de t contient un 1, alors f(t) = f(t'), t' étant le nombre obtenu en tronquant t après le premier 1 rencontré).

Dans la construction de la courbe de Hilbert, les divers carrés sont parcourus de sorte que deux carrés successifs soient toujours contigus, ce qui garantit la continuité de la courbe limite :

Si l'on parcourt les carrés, de façon plus régulière mais avec des carrés successifs non contigus, comme suit :

une construction similaire à celle de la courbe de Hilbert ne conduirait plus à une courbe à paramétrisation continue.
L'idée de la courbe de Lebesgue est de supprimer ces discontinuités en effectuant des "ponts" à l’aide de fonctions affines.

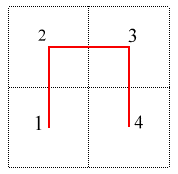
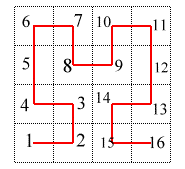
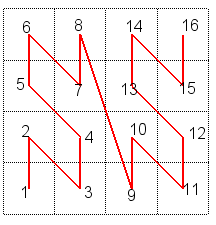
Plus précisément, à l'étape n, on obtient une suite de 4ⁿ carrés de côté , recouvrant successivement les carrés. On associe au carré le k-ième intervallede l'ensemble de Cantor approché (qui comporte bien intervalles).
Si t est un élément de l'ensemble de Cantor, le point courant de la courbe de Lebesgue est l'unique point d'intersection des compacts emboîtés , étant le rang de l'intervalle auquel t appartient. Si t n'appartient pas à l'ensemble de Cantor, il appartient à un intervalle dont seules les extrémités sont dans l'ensemble de Cantor, et l'on pose, si , .

L'on peut alors définir deux types de courbes de Lebesgue approchées qui convergent vers la courbe de Lebesgue idéale :

Premier type :
On joint successivement
les centres des
carrés
Pour n = 1
Ensemble de Cantor approché: Courbe de Lebesgue approchée :
Pour n = 2 Ensemble de Cantor approché :
Courbe de Lebesgue approchée :

Programe Maple pour le tracé du premier type :
transforme:=proc(liste,k)
local L;
L:=[op(liste),0$(k-nops(liste))]:
[seq(L[k+1-q],q=1..k)]
end:
n:=4:B:=seq(transforme(convert(k,base,2),2*n),k=0..2^(2*n)-1):
A:=seq([sum(B[k][2*q-1]/2^q,q=1..n)+1/2^(n+1),sum(B[k][2*q]/2^q,q=1..n)+1/2^(n+1)],k=1..2^(2*n)):
plot([[[0,0],[1,0],[1,1],[0,1],[0,0]],[A]],axes=none,scaling=constrained);

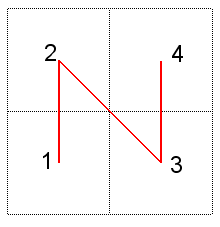
Deuxième type :
On joint successivement les points , les étant les extrémités des intervalles constituant l'ensemble de Cantor approché (qui sont les nombres de [0,1[ s'écrivant en ternaire avec 2n chiffres après la virgule égaux à 0 ou 2). Pour n = 1
Ensemble de Cantor approché:

Courbe de Lebesgue approchée :
Pour n = 2
Ensemble de Cantor approché :

Courbe de Lebesgue approchée :

Pour n = 3

premier type
deuxième type

Pour n = 4

premier type
deuxième type

Lebesgue a construit cette courbe pour donner un exemple de courbe remplissant un carré qui est non seulement continue, mais possède aussi une tangente en presque tout point (en effet la fonction est dérivable en tout t non situé dans l'ensemble de Cantor, qui est un ensemble négligeable). Il est par contre impossible de trouver une courbe remplissant un carré qui possède une tangente en tout point.

Comme la courbe de Hilbert, la courbe de Lebesgue se généralise facilement en une courbe remplissant un cube de dimension n. Par exemple en dimension 3, la paramétrisation est : posant en base 3 avec f la fonction de Cantor-Lebesgue.

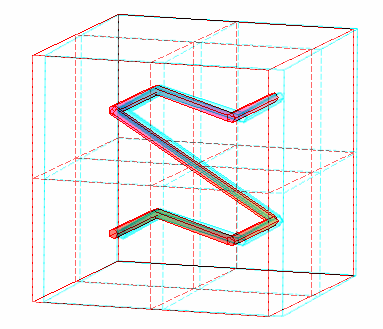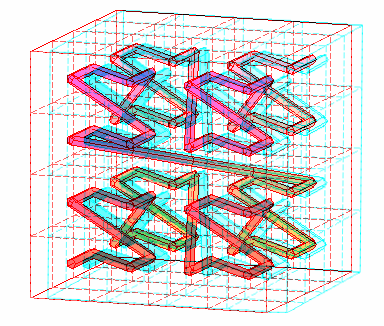Anaglyphes réalisés par alain Esculier à regarder avec des avec des lunettes rouge (à gauche) et bleu (à droite) montrant les deux premières étapes de la courbe de Lebesgue 3D (premier type).
Programme Maple (suite du précédent) :
n:=2:B:=seq(transforme(convert(k,base,2),3*n),k=0..2^(3*n)-1):
A:=seq([sum(B[k][3*q-2]/2^q,q=1..n)+1/2^(n+1),sum(B[k][3*q-1]/2^q,q=1..n)+1/2^(n+1),sum(B[k][3*q]/2^q,q=1..n)+1/2^(n+1)],k=1..2^(3*n)):
rayon:=0.02:display(spacecurve({[[0,0,0],[1,0,0],[1,1,0],[0,1,0],[0,0,0],[0,0,1],[1,0,1],[1,1,1],[0,1,1],[0,0,1]],[[1,0,0],[1,0,1]],[[1,1,0],[1,1,1]],[[0,1,0],[0,1,1]]},color=red),
tubeplot({seq(expand(t*A[k]+(1-t)*A[k+1]),k=1..2^(3*n)-1)},t=0..1,radius=rayon,grid=[2,50]),seq(plot3d(expand(rayon*[cos(u)*sin(w),sin(u)*sin(w),cos(w)]+A[k]), u=0..2*Pi,w=0..Pi,grid=[6,10]),k=2..2^(3*n)-1),lightmodel=light2,style=patchnogrid,scaling=constrained);

Voir d'autres vues stéréoscopiques du deuxième type sur cette page d'Alain Esculier (rubrique courbe de Peano, équations de G. Lavau).